「初中数学」动点产生的面积问题

【预备知识】三角形面积计算的常用策略

一、割补法

（1）若三角形至少有一边和坐标轴平行时，我们将其称为"规则"三角形

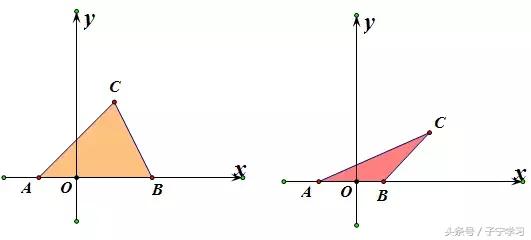
（2）若三角形三边都不和坐标轴平行时，我们将其称为"不规则"三角形

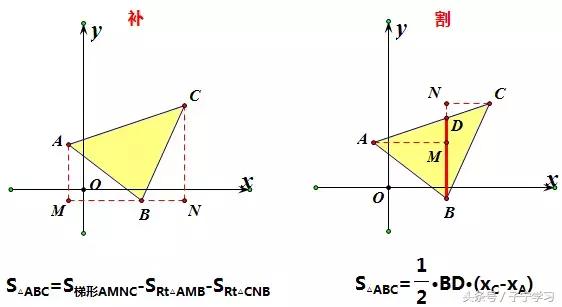
二、面积转化法

（1）借助平行线转化

（2）借助同底或同高，转化面积比

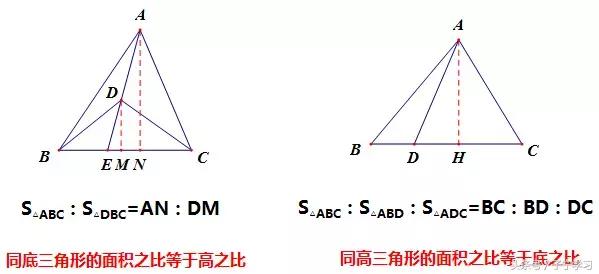
（3）借助相似三角形

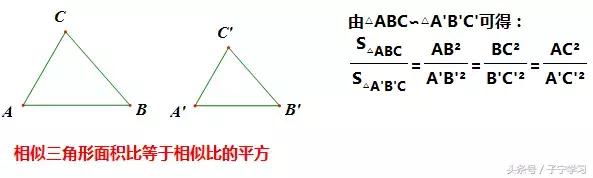
【附】常见相似结构

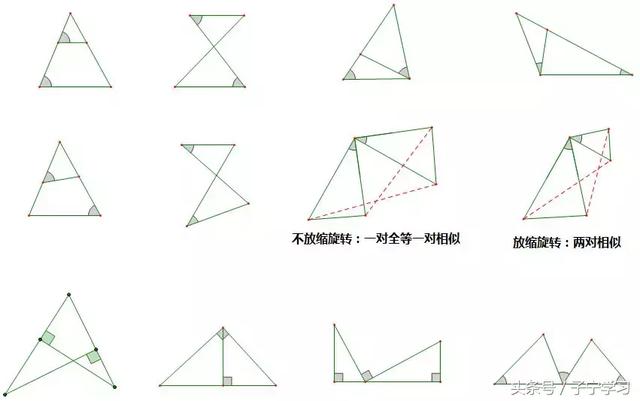
【热身训练】

1、请在直角坐标系中画出以A、B、C为顶点的三角形，并求出其面积

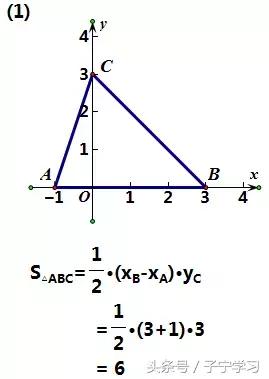
（1）A(-1,0)，B(3,0)，C(0,3)

（2）A(-1,0)，B(3,3)，C(2,4)

【解析】

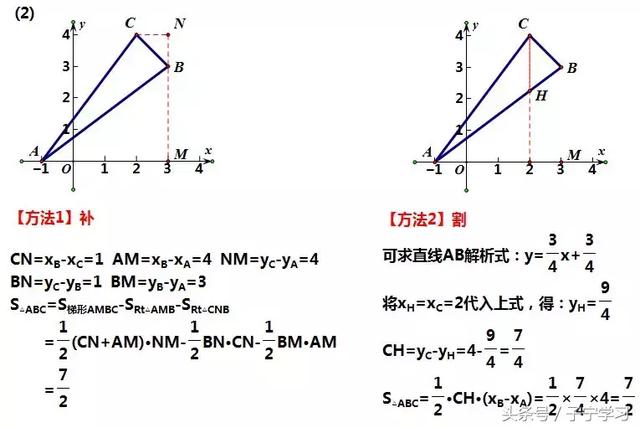
【注】

①割补法就是把"不规则"三角形，转化为"规则"三角形来解决；

②【方法1】中，我们也可以补成一个正方形；

③观察发现，AB=AC=5，可先求出BC，然后解等腰△ABC，也可解，因不属于通法，在此省略

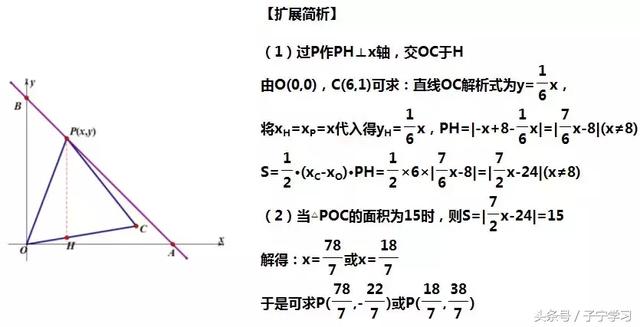
2、如图，在平面直角坐标系中，直线y=-x+8与x轴、y轴分别交于点A、B，

点P(x,y)是直线AB上一动点(点P不与点A重合)，点C(6,0)，O是坐标原点，

设△PCO的面积为S.

（1）求S与x的函数关系式

（2）当点P运动到什么位置时，△PCO的面积为15？

【解析】

【注】

①本题第(1)问也可以去绝对值，分x>8和x<8两种情况进行讨论，加上绝对值在第(2)问求解P点坐标时会省去讨论，并简化计算，但此时不要忽略x≠8(P不与A重合；

②【扩展】其他条件不变，若C坐标为(6,1)，试求上面两问

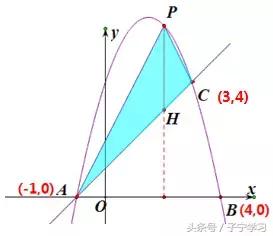
【经典例题】

【解析】

【注】

【总结与反思】

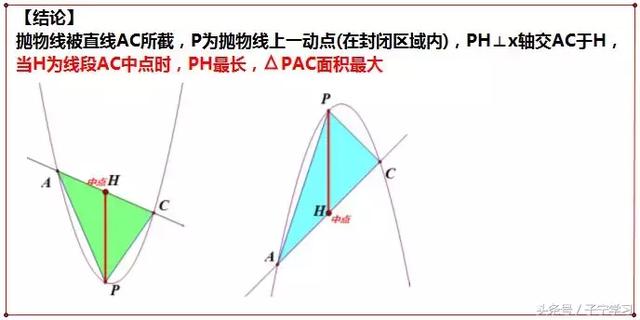
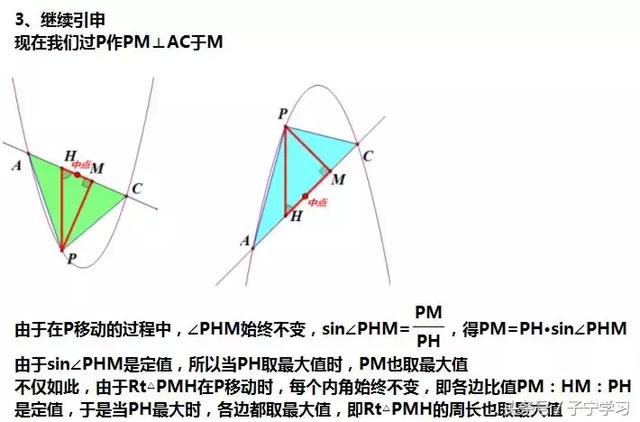
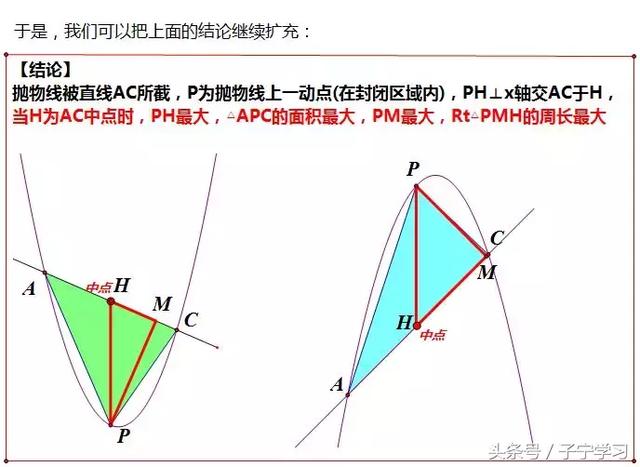
【切记】

我们推出的结论，只适合验证结论或秒杀小题，切不可在做大题时直接使用！