线段关系问题不会证？找对能得到对应关系的辅助线，才是关键

今天的全等三角形的经典例题依然是求证线段关系，那么按照《基本图形分析法》分析"三步曲"。首先，就是明白该从哪入手，也就是知晓是否添加辅助线，从而得到求证的对应相等线段。其次，根据设想的关系进行一步步的分析和证明，这其中的关键就是明白各个基本图形的性质和定义。最后，利用已证的条件应该怎么想到关键的线段相等关系。

例10 如图5-26，已知：△ABC中，∠B=60°，角平分线AD、CE相交于F。求证：AC=AE+CD。

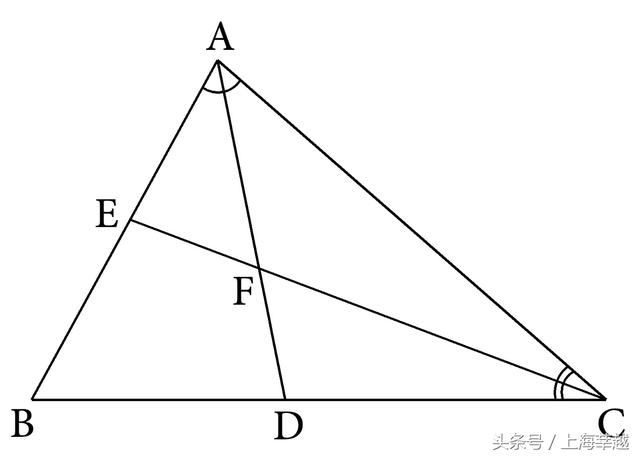
图5-26

分析：本题要证AC=AE+CD，是一条线段等于两条线段的和，所以可根据线段和的定义，在AC上截取AG=AE（如图5-27），然后证明CG=CD。

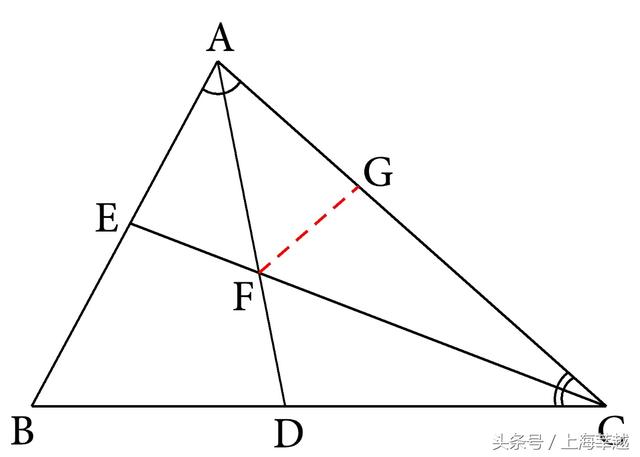
图5-27

由条件AD是角平分线，所以AG和AE这两条相等线段就是关于AD成轴对称的，从而就可添加轴对称型全等三角形进行证明，于是联结FG（如图5-27），由AE=AG，∠EAF=∠GAF和AF=AF，即可证得△EAF≌△GAF。

现在要证的结论是CG=CD，而已知CE是角平分线，所以CG、CD这两条相等线段也是关于CE成轴对称的，从而也可应用轴对称型全等三角形进行证明，也就是应证△CGF≌△CDF。而在这两个三角形中，已经有的条件是∠GCF=∠DCF，CF=CF，所以还要证明一个性质。由于CG=CD是结论，不能用。而GF=DF，即使证明了相等，出现的也是两边和其中一边的对角对应相等，还不能证明这两个三角形全等，所以第三个条件只能是证明一组角对应相等于是就应证∠DFC=∠GFC，或∠FDC=∠FCG，实际上这两个性质是等价的，所以可证明其中的任意一个。若证 ∠DFC=∠GFC，则由AD、CE相交于F，可得∠DFC=∠EFA，也就等于∠GFA，或者也就是这四个角都相等，但E、F、C成一直线，∠EFA+∠GFA十∠GFC=180°，所以问题也就成为要证∠GFC和∠DFC都等于60°

由条件∠B=60°，所以在△ABC中就可得∠BAC+∠BCA=180°-60°=120°，而AD、CE是角平分线，就有∠FAC+∠FCA=1/2·(∠BAC+∠BCA)=1/2·120°=60°，那么，在△FAC中就有∠AFC=180°-(∠FAC+∠FCA)=180°-60°=120°。而已知C、F、E成一直线，所以∠EFA=180°-∠AFC=180°-120°=60°，而∠GFA=∠EFA=60°，从而就可得∠GFC=180°-(∠EFA+∠GFA)=180°-(60°+60°)=60°，而∠DFC也等于∠EFA，所以就可得∠GFC=∠DFC，从而就可完成分析。