「中考」二次函数与三角形面积问题

【面积最大值】

每年的中考题中都会出现大量与面积有关的压轴题，要学会三角形的面积求法，并推广到任意多边形面积的求法。

这是非常重要！

【典型例题】

如图，二次函数y=-x²+2x+3与y轴， x轴交于点A ， B，

点C是直线AB上方抛物线上的一个动点（不与点A ， B重合），

求△ABC面积的最大值．

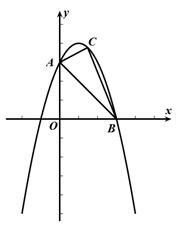
【分析】求面积的最值问题，通常设出点的动点的坐标，引入未知数来表示出面积，再利用二次函数的性质求解即可。

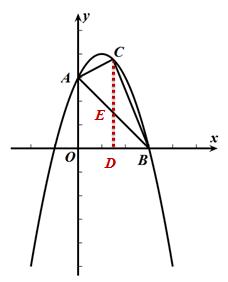
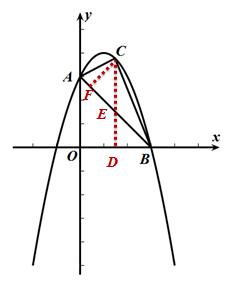
【方法一】分割——铅垂（高）法

过点C作CD⊥x轴，垂足为D，交AB于点E，

S△ABC＝ S△ACE ＋ S△BCE ＝1/2OB·CE

【方法二】补全

过点C作CD⊥y轴，垂足为D，过点B作BE⊥x轴，交CD于点E，

S△ABC＝ S矩形OBED － S△OAB － S△ACD － S△BCE

S△ABC＝ S梯形ABED － S△ACD － S△BCE

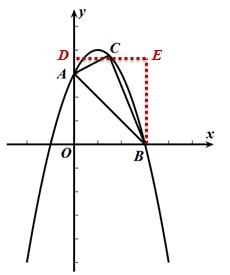
备注：本题此法繁琐，不建议用

【方法三】补全

连接OC

S△ABC＝ S△OAC ＋S△OBC － S△OAB

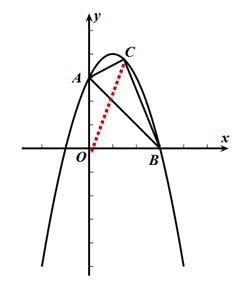
备注：此法最容易掌握

【方法四】平移

过点C作CD∥AB，分别交y轴，x轴于点D，E

S△ABC＝ S△ABD

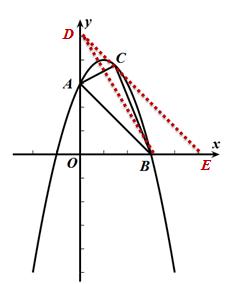
S△ABC＝ S△ABE

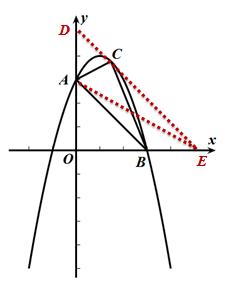
【方法五】直接求

过点C作CF⊥AB，垂足为F

S△ABC＝ 1/2AB·CF ＝ √2/4AB·CE

备注：一般此类题目皆可直接求三角形面积，用相似或三角函数表示高。

【方法六】公式法

拓展：如图，A（x1，y1），B（x2，y2），

则S△ABC＝ 1/2 |x1y2−x2y1 |

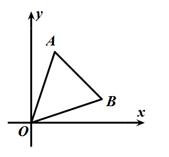
把△ABC向左平移3个单位长度，得到△OA′C′

S△ABC＝ S△OA′C′＝1/2 |xAyC-xCyA |

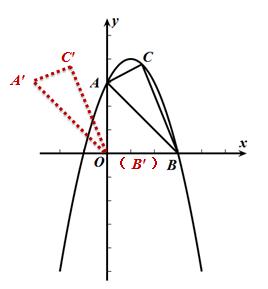
备注：以上三角形面积公式可用于选择、填空题快速求得。

发现：

当点C在OB的垂直平分线上时，S△ABC最大，

即x=(0+3)/2=3/2时， S△ABC最大

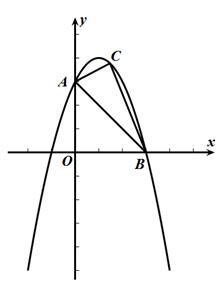
注意：点C的位置和点A、B关系密切，聪明的你，思考下，为什么会如此？

【举一反三】

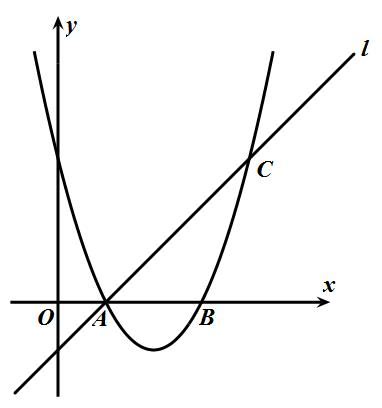
如图，已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．

（1）求抛物线的解析式；

（2）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．