「初中数学」轴对称求对称点的坐标

轴对称的妙用之对称点坐标求法

在平时的练习或考试中，同学们或许时常遇到这样的问题：在平面直角坐标系中，将某点关于一直线对称（或图形沿直线翻折），求对称点坐标。本文将此类问题归结为对称点坐标求法，并介绍两种解决此类问题的通法。

【例1】如图，在平面直角坐标系中，已知A（-1，2），B（2，0），C（0，4），求点A关于直线BC的对称点A'的坐标.

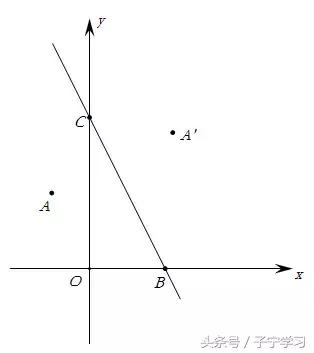
【解法一】（构造K字型）

第1步：过点A分别作x轴，y轴的平行线，交对称轴于点F, E，连接A'E,A'F。（这样做的目的是构造一个“斜直角”，即∠A‘=90°）

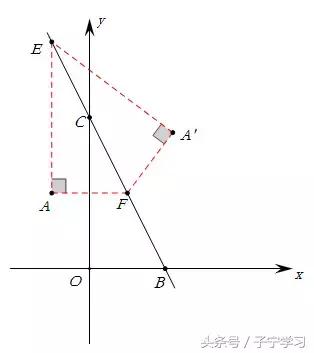
第2步：过点A’作y轴的平行线，交AF的延长线于H，过点E作A'H的垂线，垂足为K。（这样做的目的是构造矩形，并在矩形内构造“K字型”相似，即矩形大法）

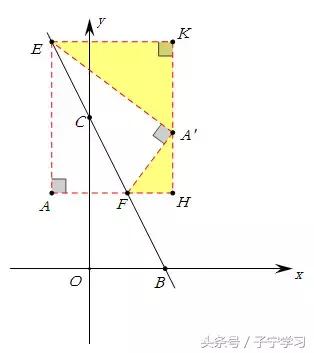
第3步：构图完毕后，接下来是一番计算，首先求出直线BC 的解析式：y=-2x+4，其次分别求出E点，F点坐标,令x=-1,解得y=6,即E（-1，6）;令y=2，解得x=1，即F（1，2），接着计算出AF=1+1=2，EA=6-2=4, 且EA:FA=EA‘：FA'=1：2.（这样做的目的是为“K字型”计算做准备）

第4步：万事俱备，只欠东风了。接下来对“K字型”进行字母表示。 ∵△EKA'∽△A'HF，且相似比为2，

∴设FH=a, 则KA’=2a,

∵KH=EA=4，∴A'H=4-2a，

∵EK=2A'H，∴EK=8-4a

∵EK=AH，且AH=1+1+a

∴8-4a=1+1+a，解得a=1.2

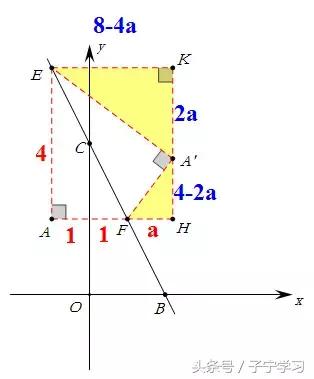
∴A’的横坐标=1+1.2=2.2 ，A‘的纵坐标为6-2a=3.6

即 A’（2.2，3.6）

【解法二】（解析法）

第1步：求出BC的解析式：y=-2x+4

第2步：因为两直线垂直, k1·k2 =–1，这里k1=-2, 所以k2 =0.5，所以设直线AA‘的解析为y=0.5x+m，将A（-1，2）代入，解得m=2.5.即直线AA'的解析式为y=0.5x+2.5

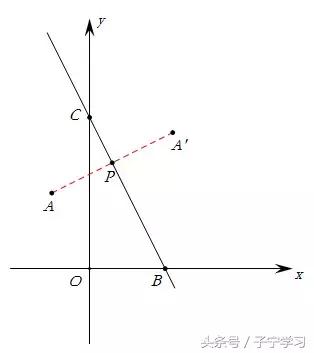
第3步：求直线BC与直线AA’的交点P的坐标。

-2x+4=0.5x+2.5, 解得x=0.6, 代入直线解析式解得 y=2.8

即P（0.6，2.8）

第4步：因为P为AA'的中点，利用中点坐标公式：

即 A’（2.2，3.6）

解题感悟

本例题介绍了求对称点坐标的两种通法，其中方法一是构造矩形，然后在矩形内构造“K字型”相似，也称作矩形大法，其优点在于计算相对简便，但在实战中构图及用字母表示相关线段是难点；方法二是解析大法，其优点是思路简单，条理清晰，但计算量相对较大，且有超纲之嫌（其中用到的两直线垂直K为负倒数；中点坐标公式都是教材外的内容）。希望同学们两种方法都能掌握，尤其是矩形大法，在很多场合都大有作为！

有道是：

对称坐标怎么求，

巧构矩形和K型。

解析大法思路清，

二者兼会更放心。