圆中常用的辅助线之一——构造直径上的圆周角

在解决与圆有关的问题时，有很多典型的、常用的辅助线，本文为你分享，通过构造直径上的圆周角来解答相关问题。

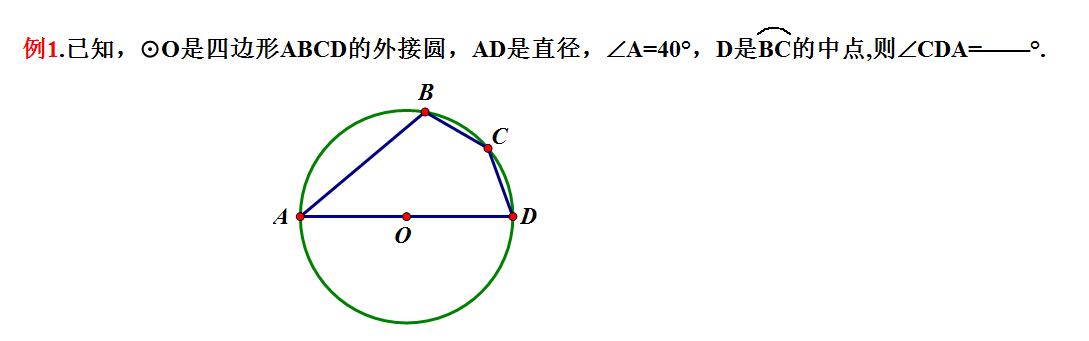
分析：本题根据已知条件“∠A=40°”，容易求得∠C的度数是140°，∠B与∠D是互补的关系。怎么求∠D呢？利用条件“AD是直径”，我们可以考虑构造“直径上的圆周角”，而要构造直径上的圆周角，此题又有两种方法，不同的构造，直接导致解答的繁简程度不同。同时，如果利用条件“D是弧BC 的中点”又有另一种添加辅助线的方法，因此，此题共有三种构造辅助线的方法.具体看下图：

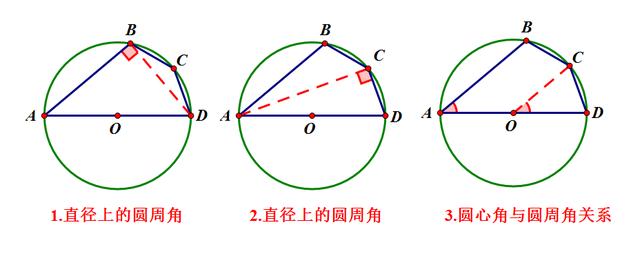
哪种构造对解答最简单？

解答留给读者。答案70°

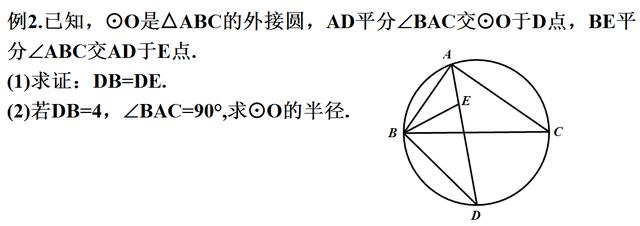
分析：第(1)小题DB、DE在同一个三角形中，可以考虑利用“等角对等边”来证明。重点分析一下第（2）小题。圆心在何处？半径(或直径)在哪里？由条件“∠BAC=90°”可知BC是直径。所以，求出BC即可得到半径。如何求BC呢？只有一条已知线段DB=4,利用地(1)小题最多能得到DE。Rt△ABC中没有已知的边啊！似乎无从着手！此时，如果想不到构造“直径上的圆周角”，那你真的会陷入困境！想得到构造这条常用的辅助线，那就容易了。看下图：

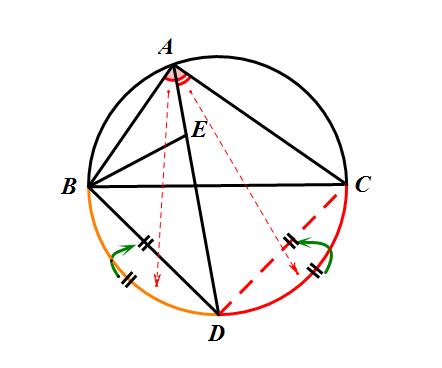
再来理一理思路：由∠BAC=90°→BC是直径→构造直径BC所对的另一个圆周角∠BDC→∠BDC=90°→同时由AD平分∠BAC→∠BAD=∠CAD→弧BD=弧CD→BD=CD=4→勾股定理求BC。

分析：还是构造直径上的圆周角，有两种不同的构造，看下图：

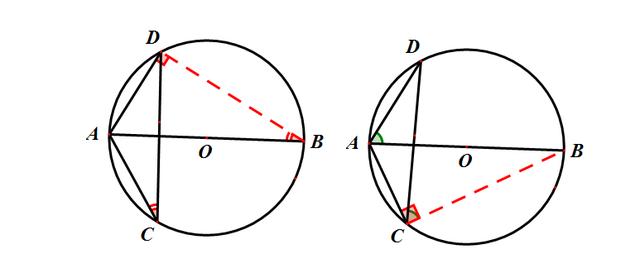
答案：60°