中考二次函数动态压轴题如何由角相等联想到相似

【思路分析】

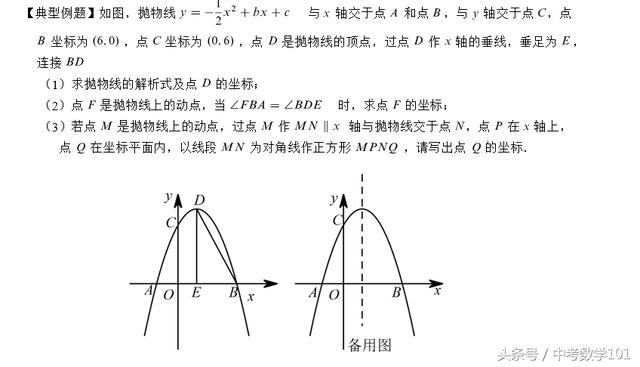
（1）中考数学二次函数压轴题第1问通常都是比较简单的，以求函数解析式、交点坐标、对称轴等为主要考点，基本属于送分题。第1问只需要将B、C两点的坐标代入解析式求出关于字母b、c的二元一次方程组就可以得到函数解析式，然后对解析式进行配方运算，最后得到顶点D的坐标D（2，8）；

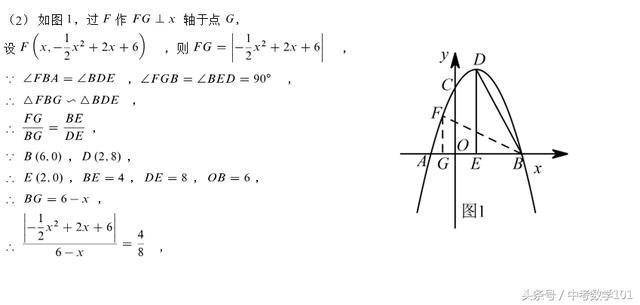
（2）第2问已知条件给的是一组相等的角，求动点F的坐标。由图形直观发现，△BDE是一个直角三角形，当∠FBA=∠BDE时，容易联想到相似三角形。这时候，借助函数简图分析，只需过点F作x轴的垂线，交x轴于点G，则△FBG∽△BDE，由此可以建立比例式FG：BG=BE：DE。第1问求出解析式后，设出动点F的坐标（x，-0.5x²+2x+6），然后将FG用参数x表示出来，由已知可求出BE=4，DE=8，OB=6，代入数据求解即可！需要注意的是点F是一个动点，因此点F可能在x轴上方，也可能在x轴下方，所以要对点F的位置进行分类讨论，为了避免漏解，用参数x表示FG的长度时候，加上绝对值符号就可以了！

（3）由题意知点M、N关于抛物线对称轴对称，并且四边形MPNQ是一个正方形，可以得到点P是抛物线对称轴与x轴的交点位置，并且点Q在抛物线的对称轴上。由此，可设出点Q（2，2n）与M（2-n，n），由于点M满足抛物线的解析式，将点M坐标代入抛物线的解析式，建立关于参数n的一元二次方程，解出n的值即可。