九年级数学相似三角形证明题中的解题技巧

一、证明相似三角形常见的几种类型

1、" A " 字型

如图所示，在 △ABC 中 ， 若 DE∥BC ，则有 △ADE∽△ABC 。

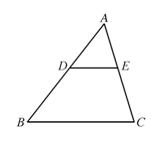
2、" A' " 型

如图所示，△ADE 和 △ABC 有公共角 ∠A ，若还有 一组对应角相等，则有 △ADE ∽△ABC 。

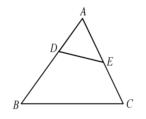
3、" 8 " 字型

如图所示， 若 AB∥CD ，则有 △AEB∽△DEC 。

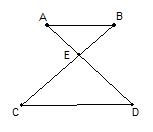
4、” 蝴蝶 “ 型

如图所示，若 ∠A = ∠C （或 ∠B = ∠D ），则有 △AEB∽△CED 。

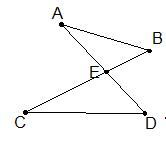
5、“ 双垂直 ” 型

如图所示，若 AC⊥BC ，（ ∠ACB = 90° ）CD⊥AB ，（ ∠CDB = 90° ） ，

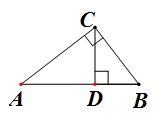
则有三组相似三角形 ：

① △ADC∽△ACB ；② △BDC∽△BCA ；③ △ADC∽△CDB 。

双垂直结论：

射影定理：

① 直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；

② 每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

⑴ ACD∽△CDB→AD:CD=CD:BD → CD^2=AD•BD ；

(2) ACD∽△ABC→AC:AB=AD:AC→AC^2=AD•AB ;

(3) CDB∽△ABC→BC:AC=BD:BC→BC^2=BD•AB ;

结论1：⑵ ÷ ⑶ 得 AC^2 ： BC^2 = AD ：BD ；

结论2：面积法得 AB•CD = AC•BC →比例式 ，证明等积式(比例式)策略 。

二、证明相似三角形常见的几种方法

1、直接法：

找同一三角形两条边和两边的夹角 ；

变化为等号同侧的两边是同一三角形中的两条边， “三点定形法 ”。

2、间接法：

⑴ 3种代换 ：① 线段代换； ② 等比代换； ③ 等积代换；

⑵ 创造条件 ：

① 加平行线 —— 创造“A”字型、“8”字型 ；

② 先证其它三角形相似 —— 创造边、角条件。

相似判定条件：两边成比夹角等、两角对应三边比（相等）。

三、例题讲解

例题1、已知在 △ABC 和 △ADE 中 ，∠ABC=∠ADE ，求证：AB·AE = AC·AD 。

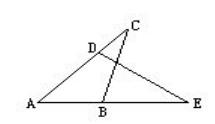
分析：

判断：本题属于 “ A‘ ” 型 ，

策略：遇等积，化比例，同侧三点找相似。

证明略 。

例题2、在Rt△ABC中，∠BAC=90°，AD⊥BC 于点 D，E 为 AC 的中点，求证：AB•AF=AC•DF 。

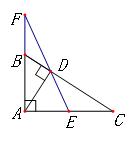
分析：本题属于 “ A‘ ” 型 和“ 双垂直” 型的综合 。

策略：斜边上面作高线，比例中项一大片，有射影，或平行，等比传递我看行。

证明：

∵ 在 Rt△BAC 中 ，∠BAC=90°，AD⊥BC ，

∴ Rt△BDA ∽ Rt△ADC ，

∴ AB : AC = BD : AD ,

∵ 在 Rt△ADC 中 ，E 为 AC 的中点 ，

∴ DE = EC ，

∴ ∠EDC = ∠C ，

∵ ∠FBD = 90° + ∠C，∠FDA = 90° + ∠FDB（ 三角形外角和定理），

又∵ ∠FDB = ∠EDC （对顶角相等）

∴ ∠FBD = ∠FDA ，

∴ △FBD ∽ △FDA ，（注：∠F 是公共角，相似中的 “ A‘” 型 ）

∴ BD : AD = DF : AF ,

∴ AB : AC = DF : AF ,

∴ AB•AF=AC•DF 。

例题3、如图所示，在平行四边 ABCD 中 ，E 为 DC 边上的一点 ，连接 BE ， 交 AC 于点 F ，延长 BE 交 AD 延长线于点 G 。

求证：BF : FG = EF : BF 。

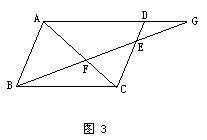
解题思路：有射影，或平行，等比传递我看行。

证明：略 。

例题4、如图所示，在 Rt△ABC 中， ∠A = 90° ，点 D、E、F、G 为三边上的点，若四边形 DEFG 为正方形。

求证：EF^2 = BE•FC 。

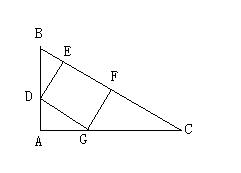
策略：四共线，有等边，必有一条可转换 。

略证：易证 △BDE ∽ △GFC （相似判定条件：两角对应相等。），

则有 BE : GF = DE : FC ,

在正方形 DEFG 中，有 DE = GF = EF ,

所以可得 EF^2 = BE•FC 。

例题5、如图所示，在 △ABC 中，AD 为 ∠BAC 的角平分线 ，求证：AB:AC=BD:CD 。（角平分线性质定理）

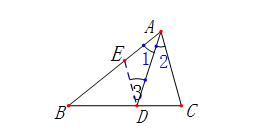
策略：两共线，上下比，两端要作平行线。（注：两共线是指求证中的线段 BD 和 CD 共线）

证明一：过点 D 作 DE∥AC ，交 AB 于点 E ，则有 △BDE ∽ △BCA （“ A ” 字型 ），

∵ △BDE ∽ △BCA ，

∴ BE : AB = DE : AC , 即 AB : AC = BE : DE ，

又∵ DE∥AC

∴ BD : CD = BE : AE (平行线分线段成比例定理），∠2 = ∠3 ，

∵ AD 为 ∠BAC 的角平分线 ，

∴ ∠1 = ∠2 ，

∴ ∠1 = ∠3 ，

∴ DE = AE ,

∴ AB:AC=BD:CD 。

证明二：过点 C 作CF∥AB ，交 AD 延长线于点 F ，则有 △ADB ∽ △FDC （ “ 8 ” 字型 ），

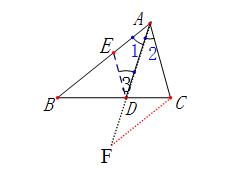
∵ △ADB ∽ △FDC ，

∴ BD : CD = AB : FC ,

又∵ AD 为 ∠BAC 的角平分线 ，

∴ ∠1 = ∠2 ，

∵ CF∥AB ，

∴ ∠1 = ∠F ，

∴ ∠2 = ∠F ,

∴ AC = CF ,

∴ BD : CD = AB : AC ,

∴ AB : AC = BD : CD 。