二次函数压轴题与常数定值问题

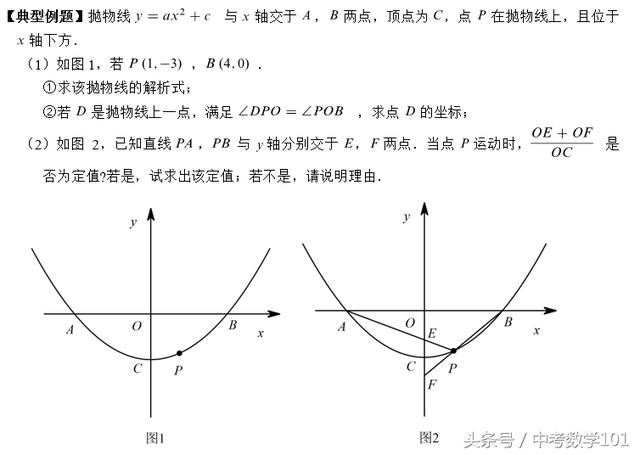
【思路分析】

（1）①二次函数压轴题第1小问，常规套路求抛物线的解析式，只需要使用待定系数法，将点P（1，3）与点B（4，0）代入抛物线的解析式y=ax²+c，解出关于a、c的二元一次方程组，求出a、c的值，可得①问答案；②由题意知，点D是一个动点，P、O、B三个点为定点，因此∠POB是一个确定的角，由图像直观，大胆猜想根据平行线的判定，可得PD//OB，由抛物线上函数值相等两点关于对称轴对称，可以求出点D的坐标；但是由于点D是一个动点，因此，连接PD交x轴于点G，当GO=GP时，正好有一个等腰三角形GOP，由此可以求出另一个点D的坐标。此处，由于点D的不确定性，容易因考虑不周造成漏解；

（2）本小问求证线段的比值是一个常数，马上观察图中有没有相似可以转化？由图形直观，发现线段OE、OF、OC都在y轴上，点E、F是随着动点P的变化而变化的，因此可以设出点P的坐标，然后过点P作PQ垂直AB于点Q，则有△BQP∽△BOF和△AOE∽△AQP，由此求出OE、OF的长度，进一步计算求解可得答案。第2问尤其注意的是，本压轴题第（1）问和第（2）问之间没有递进的关系，因此，第（1）问①中的解析式在第（2）问求解过程中是不能够使用的，只能够使用一般式。

（3）二次函数的综合题，计算与证明问题对于逻辑推理能力要求较高，需要我们有扎实的数学功底，才能够顺利破解中考压轴题。