「初中数学」几何图形中点遇到手拉手

【原题再现】

如图，ABCD为正方形，△CEF为等腰直角三角形，连接AE、AF，M是AE中点，DM交AF于N，求证：DN⊥AF

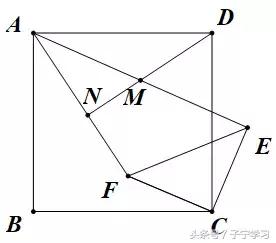
【前导知识及分析】

1、中点模型构造策略

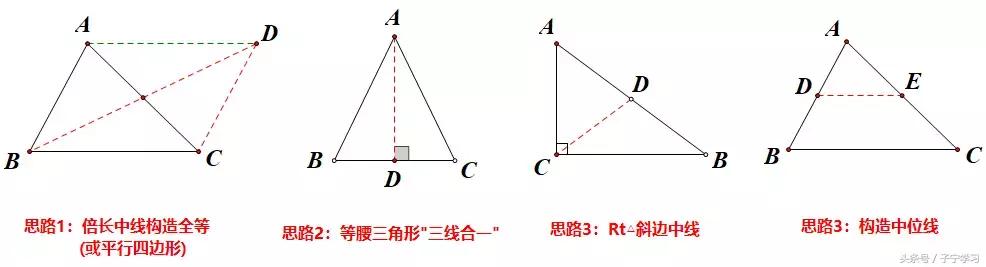
2、"手拉手"模型("旋转一拖二")构造策略

"手拉手"模型的雏形（前提条件）

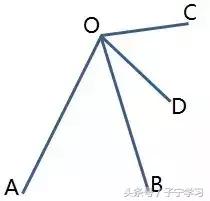
线段关系：OA=OB，OC=OD

角关系：∠AOB=∠COD，∠AOD=∠BOC(旋转一拖二的理论基础)

3、本题分析

本题中有两个重要条件：

①"M是AE中点"——为构造"中点模型"提供前提条件

②"△CEF为等腰直角三角形"(CF=CE)——为"手拉手"模型("旋转一拖二")提供前提条件

<静态来看>：

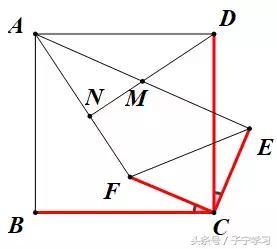
图中含有"手拉手"模型的雏形

<动态来看>：

【方式1】CF带动△FCB绕C顺时针旋转90°

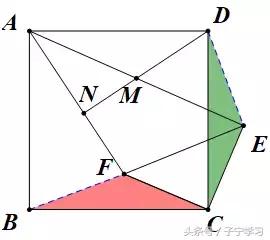
很明显，△BFC≌△DEC

于是得到：

①BF=DE(为构造"中点模型"搭桥)

②∠FBC=∠EDC(用于导角)

【方式2】CF带动△AFC绕C顺时针旋转90°

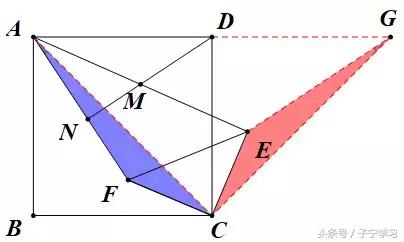
很明显，我们能观察到：△AFC≌△GEC

于是得到：

①AF=EG(为构造"中点模型"搭桥)

②∠FAC=∠EGC(用于导角)

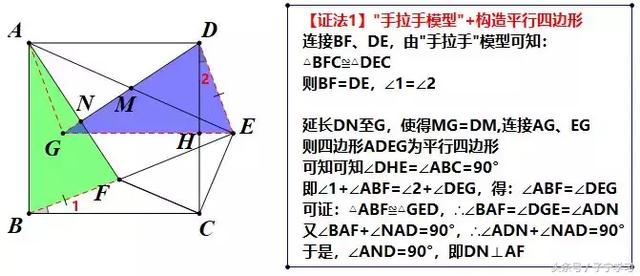
【注】

在理解"手拉手"模型的前提下，想到连接DE、BF，那么DM即为△ADE的中线，自然想到倍长中线法，为省去一组全等三角形的判定，不如直接构造平行四边形(两组对边分别平分)，AD=GE=AB，再加上BF=DE，自然构思彩色三角形全等，进而证取结论。在群内研讨时，有很多老师觉得这个构思很巧妙，甚至觉得有点不可思议。但笔者却认为，与下面几种方法相比，【证法1】是大家应该首先想到的，其构思是顺理成章的，因为它都来源于通用的方法——"旋转一拖二"和"倍长中线构平四"

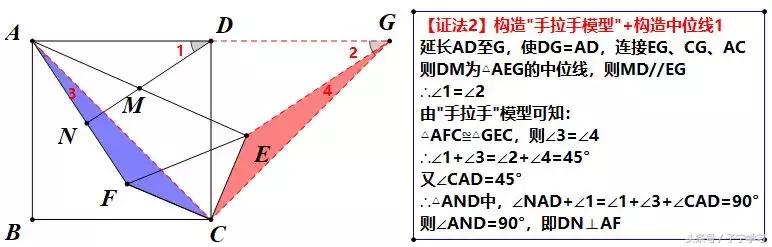
【注】

如果我们以动态的观点(旋转)来看待这个问题，CF带动△AFC绕C顺时针旋转90°，得到△GEC，旋转角为90°，即对应边的夹角为90°，∠FCE=∠ACG=90°，而AF的对应边是GE，那么它们的夹角也应该是90°，也就是说GE⊥AF，通过中位线构造，我们知道DN//GE，于是我们没有导角的情况下，就得到了DN⊥AF，是不是感觉很美妙那？

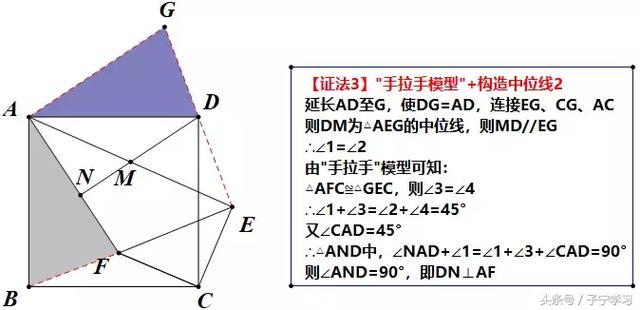
【注】

与【证法2】类似，如果我们仍以动态的观点(旋转)去看待，AB带动△ABF绕A逆时针旋转90°，我们同样可以得到AG⊥AF，再由AG//DN，得到DN⊥AF

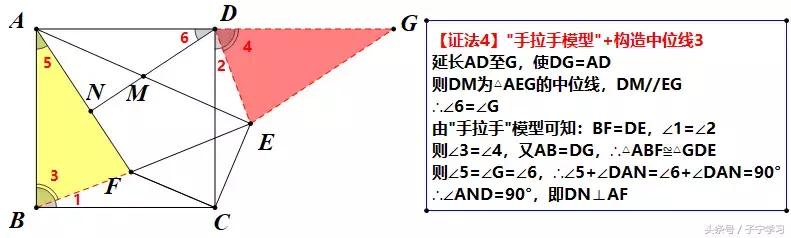
【注】

与【证法2】类似，如果我们仍以动态的观点(旋转)去看待，BA带动△ABF绕B顺时针旋转90°，之后平移得到△GDE，由于平移不改变对应边的夹角，即原旋转角不变，得AF⊥GE，又DN//GE，于是，DN⊥AF

【注】

由于ABCD为正方形，自然想到取其中心O与M，联系构造中位线，之后无意中发现：MP：CE=DP：AC=1:2，于是想到构造相似三角形

动态观点：旋转+放缩平移(位似)

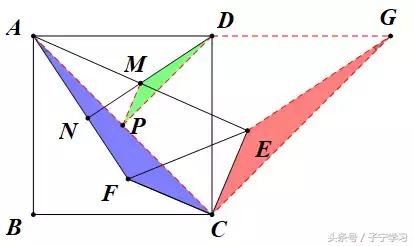
EG⊥AF，EG//DN，得DN⊥AF

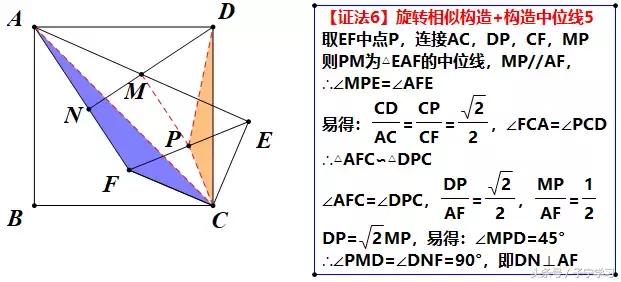
【注】

取EF中点P，与M联系构造中位线，发现CP:FC=CD:AC=2:√2，于是想到构造相似三角形

动态观点：FC绕点C带动△AFC顺时针旋转45°，则AF与DP夹角也为45°，MP//AF，则MP与DP夹角也为45°，即∠MPD=45°，联系线段比得到△MPD为直角三角形

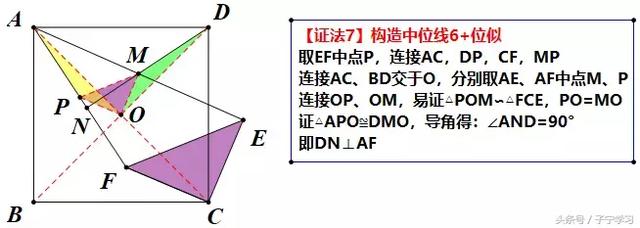
【注】

和【证法5】相反，此证法是先放缩平移(位似)，再进行旋转，

静态观点：

通过位似，我们也能轻易看到"手拉手"模型的雏形

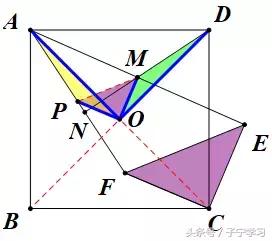
【谈谈反思和收获】

1、"一题多解"——本题解法大致分为三类：倍长中线构平四、中位线+旋转全等构造，中位线+旋转相似构造

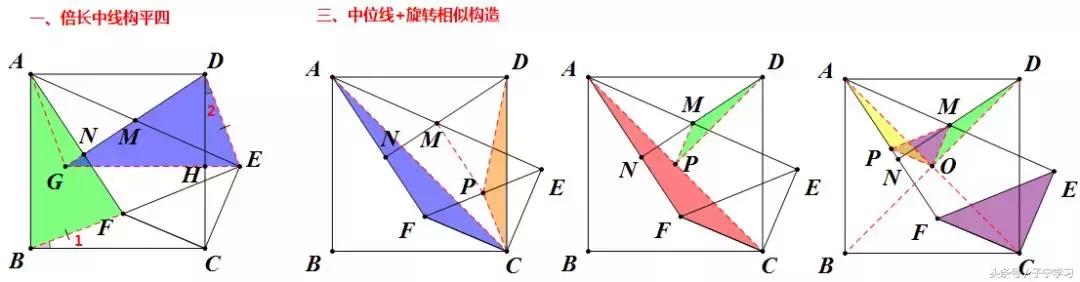
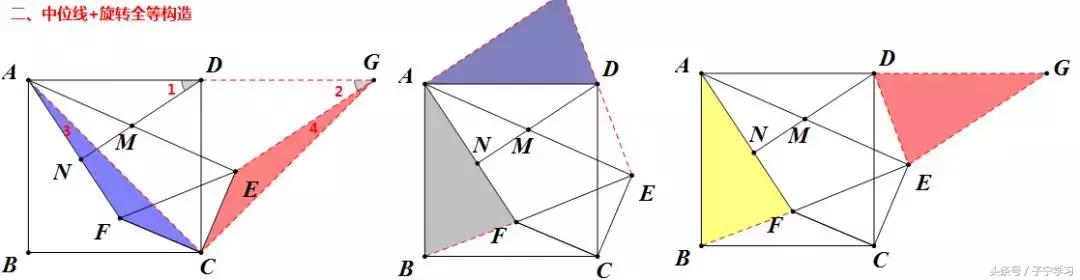
2、"多解归一"——本例的突破口及核心思想是什么？

很明显，本题的关键条件为——"M是AE中点"，以此为突破口联想构造中点模型(倍长中线/中位线)，另外在旋转的观点构造全等或相似时，由于证明的结论为DN⊥AF，在旋转时，自然想到跟AF扯上关系，带动其旋转90°，得到新的线段(记为A'F')，只需证明A'F'//DN，即可说明DN⊥AF，这正是其核心思想。