专题1、角平分线四种常见辅助线添加方法

角平分线具有两条非常重要的性质：一是对称性；二是角平分线上的点到角两边的距离相等。

对于有角平分线的辅助线的作法，一般有四种：

①从角平分线上一点向两边作垂线；②利用角平分线，构造对称图形（如作法是在一侧的长边上截取短边）；③做角平分线的垂线，与角两边构造等腰三角形；④过角平分线上的点做边的平行线。

方法一、在证明线段的和差倍分问题中，常用到的方法是延长法或截取法来证明，以此来构造三角形全等，

延长短的线段，或在长的线段上截取一部分，使之等于短的线段。但无论延长，还是截取都要证明线段的相等。

延长要证明延长后的线段与某条线段相等，截取要证明截取后剩下的线段与某条线段相等，进而达到所要证明的目的。

例2中，用到了角平分线，用到了做垂直，利用三线合一证明边相等，利用SAS来证明三角形全等。

此题的证明，也可以在AB上截取AE=AC，先证明△ADE≌△ADC，再利用AB=2AC，得出E是AB的中点，再利用三线合一证明DE⊥AB，所以DC⊥AC.

课后专项练习一，就是利用延长或者截取法，来证明的。

题目不难，非常基础，请同学们，认真仿照例题，认真推敲，加强练习。

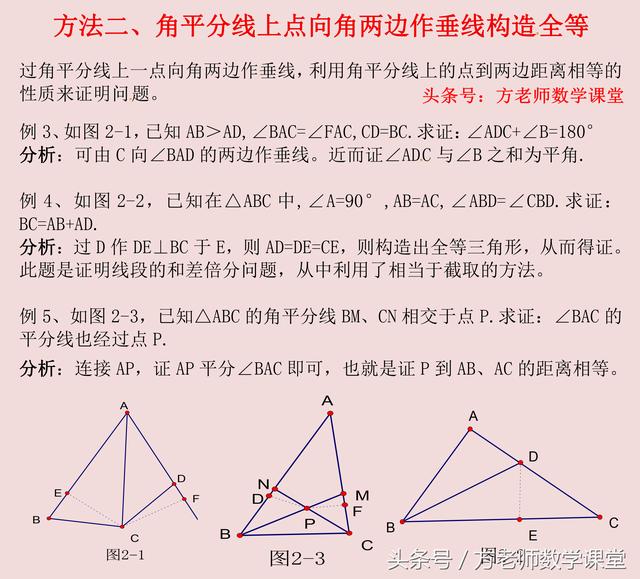
方法二、角平分线上的点向角两边做垂线。通常情况下，出现了直角或是垂直等条件时，一般考虑作垂线；

其它情况下考虑构造对称图形。至于选取哪种方法，要结合题目图形和已知条件。

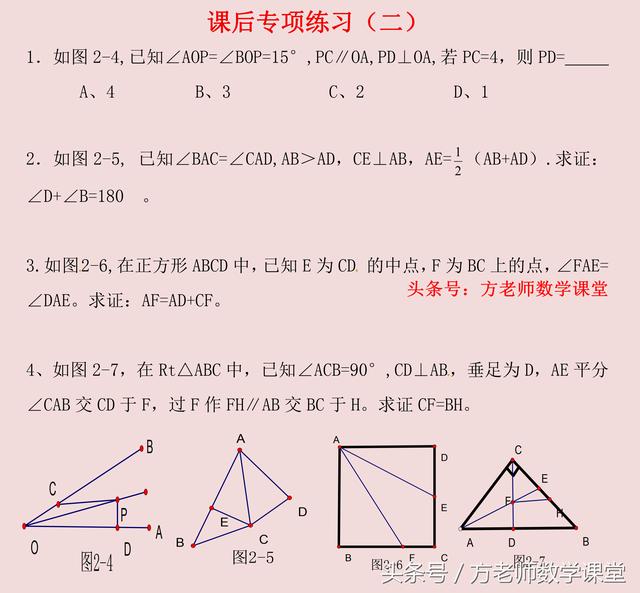
一般来说，出现角平分线，做双垂直，都是非常通用的方法。

要么过角平线上的点做角两边的垂直，要么做角平分线的垂直交两边，都是必出三角形全等。

方法三，过角平分线上的一点，做角平分线的垂线，必然交于角的两边，构造出等腰三角形。这个方法，在很多题型中，非常实用。

专项练习三，有两个题，需要自行画图。只要我们一个专题一个专题的突破，把基础扎实起来，那么初中几何还难吗？初中数学还难吗？

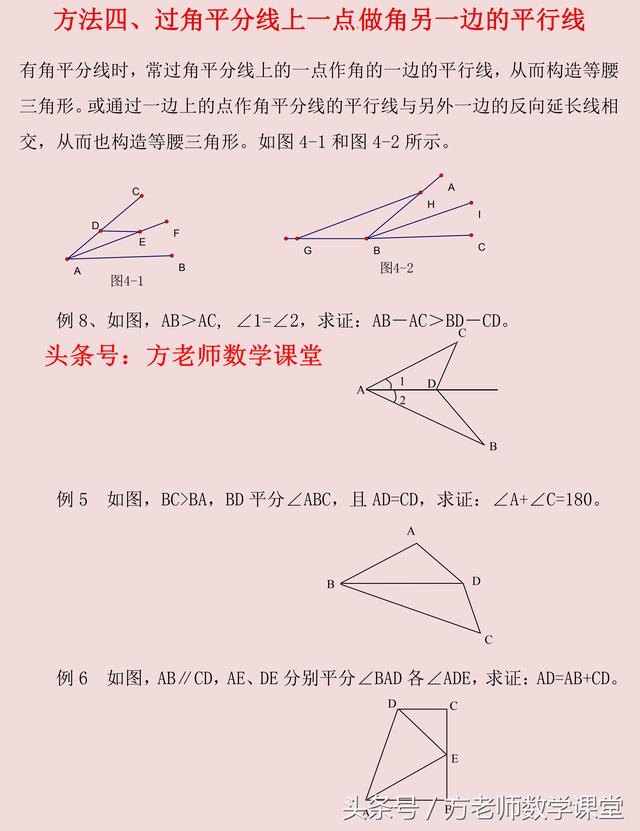
方法四、过角平分想上一点，做角的另一边的平行线。

因为角平分线有两角相等，平行线则有内错角相等，则必然出现角相等，得等腰三角形。