九年级数学二次函数压轴题解析一例（6）

例题7、（2018年包头市中考数学第26题）如图，在平面直角坐标系中，已知抛物线

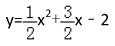
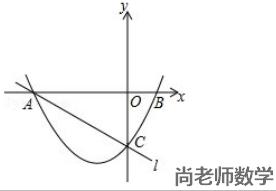
与 x 轴交于 A 、 B 两点，（点 A 在点 B 的左侧），与 y 轴交于点 C ，直线 L 经过 A 、C 两点 ，连接 BC 。

（1）求直线 L 的解析式 ；

（2）若直线 x = m （m < 0）与该抛物线在第三象限内交于点 E ，与直线 L 交于点 D ，连接 OD ，当 OD⊥AC 时，求线段 DE 的长 ；

（3）取点 G（0，-1），连接 AG ，在第一象限内的抛物线上，是否存在点 P ，使 ∠BAP = ∠BCO - ∠BAG ？若存在，求出点 P 的坐标；若不存在，请说明理由 。

解题思路：

（1）由抛物线的解析式可以求出点 A 、点 C 的坐标， 从而可以求出直线 L 的函数解析式 ；

（2）根据题意作出合适的辅助线，利用三角形相似和勾股定理来解答本题 ；

（3）根据题意画出相应的图形，利用锐角三角函数求出 ∠OAC = ∠OCB ，然后根据题目中的条件和图形，利用锐角三角函数和勾股定理即可解答本题 。

解答过程：

（1）∵ 抛物线 y = 1/2 x^2 + 3/2 x - 2 ,

∴ 令 y = 0 时 ， 解得：x1 = 1 , x2 = 4 ；令 x = 0 时, 解得： y = -2 。

∵ 抛物线 y = 1/2 x^2 + 3/2 x - 2 与 x 轴交于 A 、 B 两点，（点 A 在点 B 的左侧），与 y 轴交于点 C ，

∴ 点 A 的坐标为（-4,0），点B（1,0），点C（0,-2），

设经过 A 、C 两点直线 L 的函数解析式为 y = kx + b ( k ≠ 0 ) , 则有

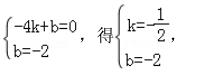
∴ 直线 L 的函数解析式为 y = -1/2 x - 2 ；

（2）直线 ED 与 x 轴交于点 F ，如图1所示，

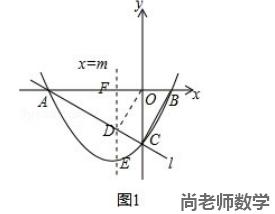
由（1）可得：OA = 4 , OC = 2 , ∠AOC = 90° ，

在 Rt△AOC 中，由勾股定理可得：AC = 2√5 ，

∵ OD⊥AC ， AO⊥OC ，∠OAD = ∠CAO ，

∴ 1/2 × OA × OC = 1/2 × OD × AC ，OD = 4×2 /（2√5）= 4√5/5 ，

∴ △AOD∽△ACO ，

∴ AD/AO = AO/AC , 即 AD/4 = 4/(2√5) , 解得：AD = 8√5/5 。

又∵ EF⊥x 轴，∠AOC = 90° ，∴ EF∥OC ，

∴ △ADF∽△ACO ，

∴ AF/AO = FD/OC = AD/AC , 解得：AF = 16/5 , DF= 8/5 ，

∴ OF = 4 - 16/5 = 4/5 ,

∴ m = -4/5 ,

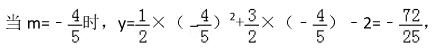
∴ EF = 72/25 ,

∴ DE = EF - FD = 72/25 - 8/5 = 32/25 ；

（3）存在点 P ，使 ∠BAP = ∠BCO - ∠BAG 。

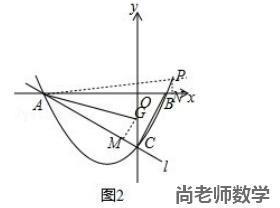
理由如下：作 GM⊥AC 于点 M ，作 PN⊥x 轴于点 N ，如图2所示，

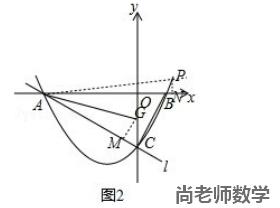
∵ 点 A（-4,0），点 B（1,0），点 C（0，-2），

∴ OA = 4 , OB = 1 , OC = 2 ,

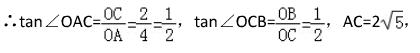
∴ ∠OAC = ∠OCB ，

∵ ∠BAP = ∠BCO - ∠BAG （已知条件假设存在），∠GAM = ∠OAC - ∠BAG ，

∴ ∠BAP = ∠GAM ，

∵ 点 G（0，-1），AC = 2√5 , OA = 4 , ∴ OG = GC = 1 ,

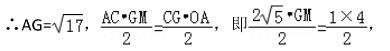
解得：GM = 2√5/5 ，

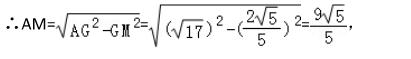
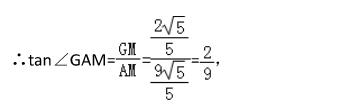
∴ tan∠PAN = 2/9 , ( 前面结论已知 ∠BAP = ∠GAM )

设点 P 的坐标为

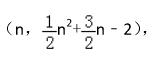
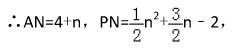
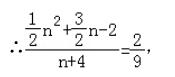
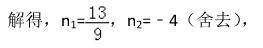
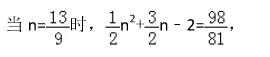
∴ P 点的坐标为 （13/9 , 98/81）, 即存在点 P（13/9 , 98/81）, 使 ∠BAP = ∠BCO - ∠BAG 。