中考数学压轴题二次函数中动点与线段的长度

【思路分析】

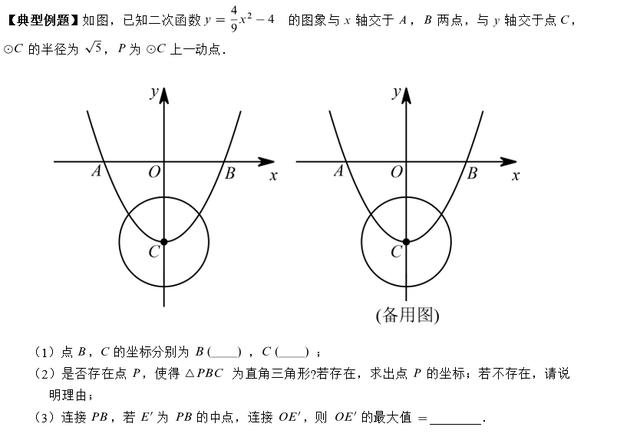
（1）二次函数综合题目第1问属于基础题，一般以求抛物线与坐标轴的交点、对称轴、解析式为主，只要细心求解即可。在抛物线解析式中令y=0，可求得A、B点坐标，令x=0可以求得C点的坐标；

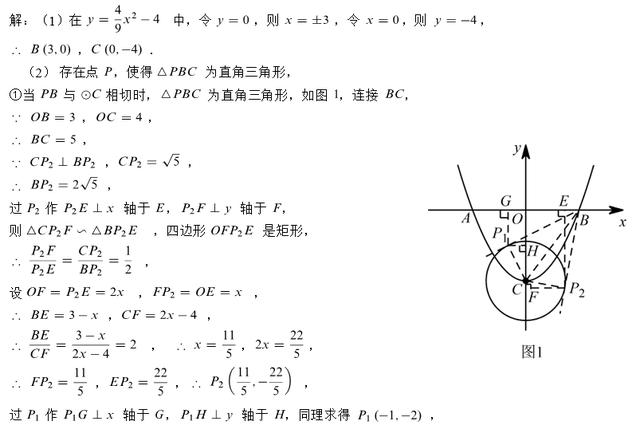
（2）第2问中，给出三角形PBC是直角三角形，但是没有明确的说明哪个角是直角，所以需要分类讨论。其中点B不可能是直角顶点，因此只需要分点P和点C是直角顶点两种情况分类讨论。

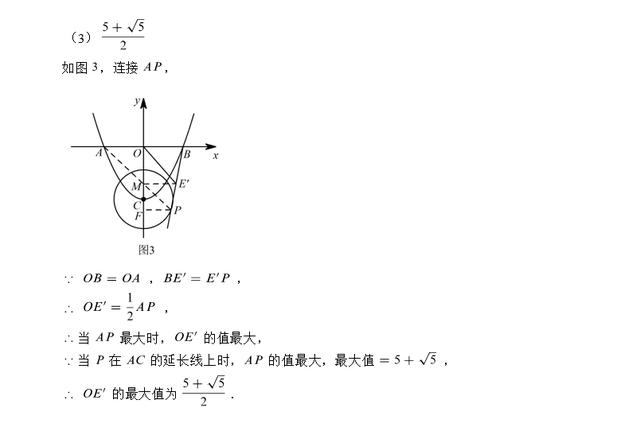
（3）由题意得，点B是固定的点，点P是圆C上的一个动点，并且点E’是PB的一个动点，因此点P在运动的过程中，点E’也跟着运动，但是始终保持着一个条件成立“E’是PB的中点”不变，由此可知点E的运动轨迹也是一个圆。由中点我们容易展开联想知识点——三角形中位线。仔细观察图形可以得出，点O是线段AB的中点，因此可以连接线段PA，三角形ABP的中位线就是线段OE，则由三角形中位线的性质，当AP取得最大值时，OE’也取得最大值。则圆外一点到圆上各点的连线段中，经过圆心的线段与圆相交于两点，一个点是满足AP最大的，一个点是满足AP最小的，由此可以得出题目所求结论。

（4）本题是二次函数的综合应用题，涉及函数的解析式求点的坐标、相似三角形、勾股定理、三角形的中位线、直线与圆的位置关系等相关知识点，考查了方程、分类讨论、转化思想，综合性强，区分度较高。其中，第3问难度较大，需要我们细心画图分析，在草图中寻找几个定点E的位置，一步步寻找解题的思路。最后，只要我们能够发现隐形圆，借助三角形的中位线将问题转化为“圆外一定点到圆上距离的最值”问题，第3问迎刃而解。