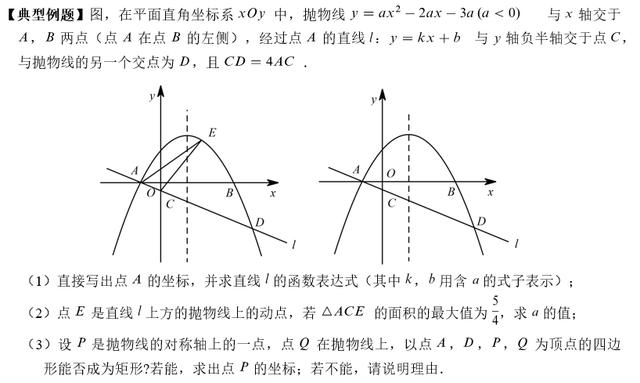
【思路分析】
(1)由于抛物线的解析式y=ax²-2ax-3a中每一项都含有a,所以令y=0,得ax²-2ax-3a=0,即x²-2x-3=0,由此可以得到抛物线与x轴的两个交点A、B的坐标。已知CD=4AC,因此可以联想到相似比,故将其转化为点A、D横坐标之间的数量关系,再根据点D是直线与抛物线的交点,从而求出直线的解析式;
(2)我们经常练习求解二次函数与三角形面积的最值问题,现在给出最大值反而会让部分同学不知道如何下手。我们可以根据解“二次函数中动点与三角形面积最值”的方法,先建立三角形ACE面积的函数表达式,求出三角形面积的表达式,然后比较得出的面积最大值,再求参数a的值;
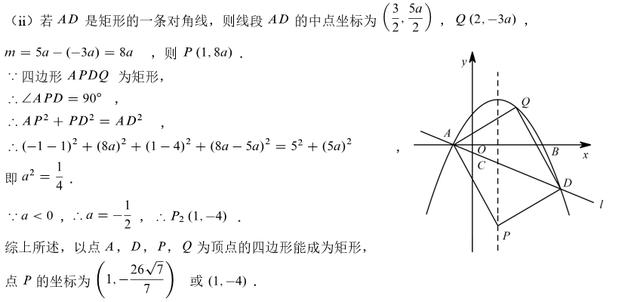
(3)对于动点问题,我们要多动手画示意图,根据图形展开探索,勤思勤练解题思维自然成。以点A、D、P、Q为顶点的四边形能否构成矩形?习惯的做法当然是假设存在,然后分类讨论,尝试画出图形,结合矩形的性质,由线段互相垂直可以找到直角三角形,则勾股定理可用,进一步联想到角的互余、是否暗示有相等的角、有没有相似图形等。通过画图分析可知,AD可能是矩形的一条边或是矩形的一条对角线,由此展开分类讨论求解即可。
(4)本题是二次函数的综合题,综合性较强,解题的关键在于解题思路的选择,多看多思考方能引导我们一步一步地发现正确而简洁的解题思路,同时还要注意数形结合思想、转化思想、分类讨论思想以及方程思想的应用,要学会用符号语言有条理地将解题思路叙述出来。


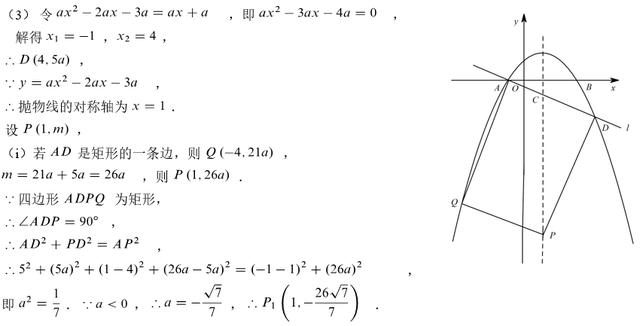

 加载中,请稍侯......
加载中,请稍侯......
精彩评论