中考数学压轴题专训二次函数中动点与相似三角形

【思路分析】

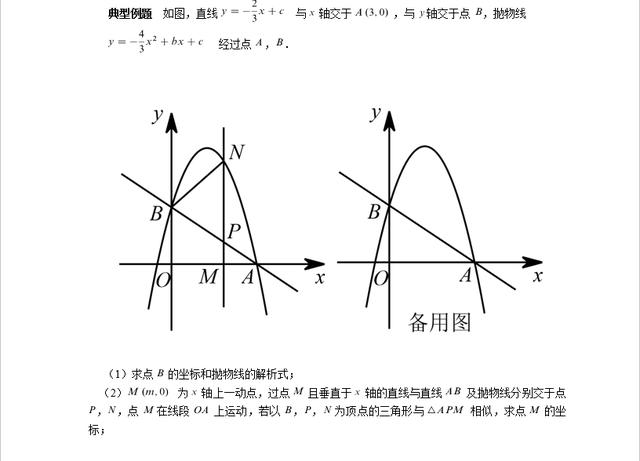
本题是二次函数综合题，主要涉及二次函数解析式、函数图像的交点、相似三角形的性质和判定、勾股定理、线段的中点坐标等知识，涉及方程思想与分类讨论思想等数学核心知识。第（1）小 问利用待定系数法，将 A 坐标代入直线解析式可求得 c 的值，由此再求得直线与 y 轴的交点坐标；求出 A、B 两点的坐标后，代入二次函数解析式可求得参数 b 的值。（2）中的点 M（m，0）在 线段 OA 上运动，所以 0≤m≤3，过点 M 且垂直于 x 轴的直线上所有的点横坐标相同，均为 m，由此可得 P、N 两点的坐标，进一步用两点间的距离公式可以表示出 MA、MP、PB、PN 的长度。 由于以 B、P、N 为顶点的三角形与△APM 有一对对顶角相等，对于明显找出一对对应角相等的两个三角形相似的问题，通常是利用“两边对应成比例且夹角相等的两个三角形相似”建立参数方程。如果注意到△APM 为直角三角形且与确定的△ABO 相似，那么△BPN 也必定是一个直角三角形。因此，当∠NBP=90°或∠BPN=90°时，两个三角形相似，从而将相似问题转化为直角三角形的问题进行分类讨论，因而第 2 小问也容易因为考虑不全面而导致漏解。具体解答过程如下：