函数中动点与四边形面积最大值

【思路分析】

（1）根据已知条件中，当自变量x=-1和x=5时，函数值是相等的可以求出抛物线的对称轴为x=2，再把对称轴方程和直线l的方程联立，可以求得抛物线的顶点坐标，由此我们可以设出抛物线的顶点式，然后代入点（3，-4），只要细心运算就可以求出抛物线的解析式；但是部分同学可能无法理解“当自变量x=-1和x=5时，函数值是相等”发现隐藏的对称轴，导致思维停顿，或陷于复杂的运算当中，说明对抛物线的图像与性质还不能够灵活运用；

（2）先求出抛物线与y轴交点C的坐标，然后从特殊的情况开始研究。当角PCO和角ACO相等的时候，求出相应的点P的坐标。过点A作关于y轴的对称点A’，连接CA’交抛物线于点P，则可以知道三角形ACA’是一个等腰的三角形，通过联立方程组可以得到交点P的坐标。接着观察图形，得到结论，但是要特别注意角PCO是一个锐角。我们研究数学问题往往都是从特殊到一般的过程，选择从特殊的点入手，数形结合，用相等解决不等的问题；

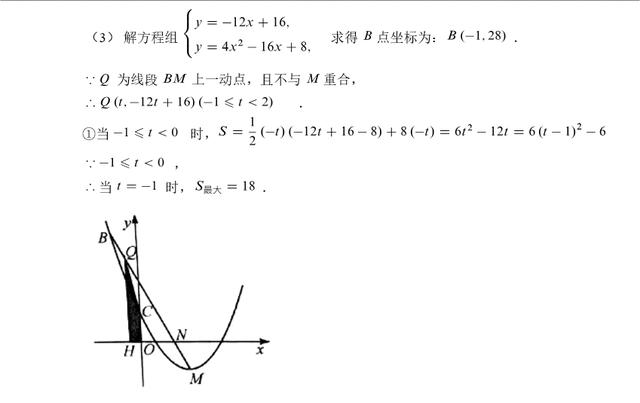
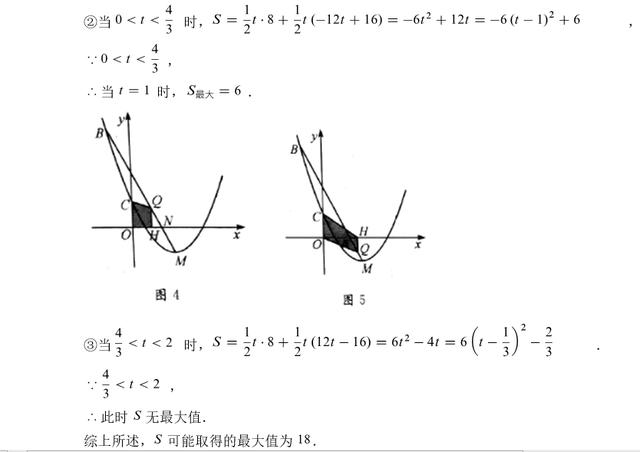
（3）先求出直线l与抛物线另一个交点B的坐标，点Q（t，n）为线段BM上一个动点（点Q不与M重合），所以可以求出参数t的取值范围是-1≤t＜2。通过草图分析，发现以Q、H、O、C四个点为顶点的四边形形状是不断变化的，这里需要分三种情况讨论。第一种情况是-1≤t＜0时，第二种情况是t大于0而小于三分之四，第三种情况是t大于三分之四而小于2，然后进一步计算求得答案。

（4）本题考查待定系数法求抛物线解析式，等腰三角形的性质和判定、二次函数图像与性质等相关知识，难度在于题目的分析草图要自己动手画，图形动态变化的过程不好观察，还需要局部放大，进行合理的想象，从而明确分类讨论的标准。