典型例题分析1:
在0,1,﹣2,3这四个数中,最小的数是( )
A.﹣2 B.1 C.0 D.3
解:∵﹣2<0<1<3,[来源
∴最小的数是﹣2,
故选:A.
题干分析:
根据正数大于负数,两个负数比较大小,绝对值大的数反而小,可得答案.
解题反思:
本题考查了有理数比较大小,正数大于0,0大于负数是解题关键.
典型例题分析2:
下列计算中,结果是a6的是( )
A.a2+a4 B.a2•a3 C.a12÷a2 D.(a2)3
解:∵a2+a4≠a6,
∴选项A的结果不是a6;
∵a2•a3=a5,
∴选项B的结果不是a6;
∵a12÷a2=a10,
∴选项C的结果不是a6;
∵(a2)3=a6,
∴选项D的结果是a6.
故选:D.
考点分析:
同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
题干分析:
A:根据合并同类项的方法判断即可.
B:根据同底数幂的乘法法则计算即可.
C:根据同底数幂的除法法则计算即可.
D:幂的乘方的计算法则:(am)n=amn(m,n是正整数),据此判断即可.
典型例题分析3:
下列说法错误的是( )
A.角平分线上的点到角的两边的距离相等
B.直角三角形斜边上的中线等于斜边的一半
C.菱形的对角线相等
D.平行四边形是中心对称图形
解:∵角平分线上的点到角的两边的距离相等,
∴选项A正确;
∵直角三角形斜边上的中线等于斜边的一半,
∴选项B正确;
∵菱形的对角线互相垂直,但是不一定相等,
∴选项C不正确;
∵平行四边形是中心对称图形,
∴选项D正确.
故选:C.
典型例题分析4:
某同学晚上6点多钟开始做作业,他家墙上时钟的时针和分针的夹角是120°,他做完作业后还是6点多钟,且时针和分针的夹角还是120°,此同学做作业大约用了( )
A.40分钟 B.42分钟 C.44分钟 D.46分钟
解:设开始做作业时的时间是6点x分,
∴6x﹣0.5x=180﹣120,
解得x≈11;
再设做完作业后的时间是6点y分,
∴6y﹣0.5y=180+120,
解得y≈55,
∴此同学做作业大约用了55﹣11=44分钟.
故选C.
典型例题分析5:
如图1,已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作,将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转,再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…,如图2,是六次旋转的位置图象,图中虚线是点M的运动轨迹,则在第四次旋转的过程中,点B,M间的距离可能是( )
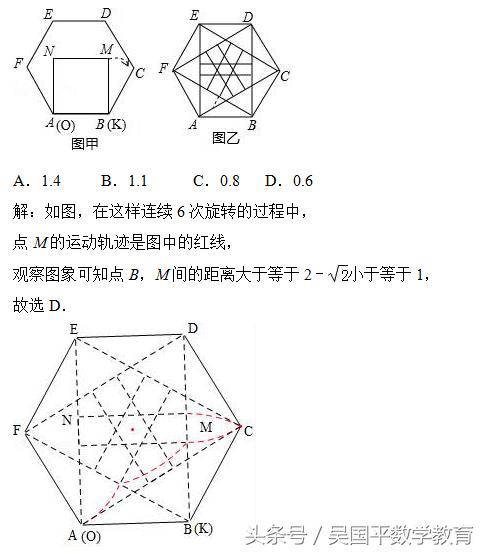

 加载中,请稍侯......
加载中,请稍侯......
精彩评论