中考数学：与二次函数相关的解解答题

典型例题分析1：

已知二次函数y=x2+bx+c（b，c为常数）．

（1）当b=2，c=﹣3时，求二次函数图象的顶点坐标；

（2）当c=10时，若在函数值y=1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；

（3）当c=b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．

考点分析：

待定系数法求二次函数解析式；二次函数的最值．

题干分析：

（1）把b=2，c=﹣3代入函数解析式，求二次函数的最小值；

（2）根据当c=10时，若在函数值y=l的情况下，只有一个自变量x的值与其对应，得到x2+bx+5=1有两个相等是实数根，求此时二次函数的解析式；

（3）当c=b2时，写出解析式，分三种情况进行讨论即可．

典型例题分析2：

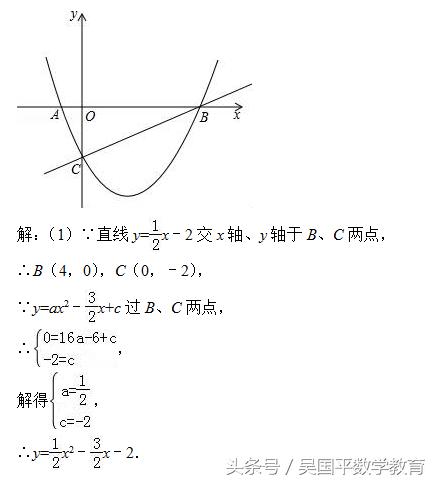
如图，已知抛物线y=ax2﹣3x/2+c与x轴相交于A、B两点，并与直线y=x/2﹣2交于B、C两点，其中点C是直线y=x/2﹣2与y轴的交点，连接AC．

（1）求抛物线的解析式；

（2）证明：△ABC为直角三角形；

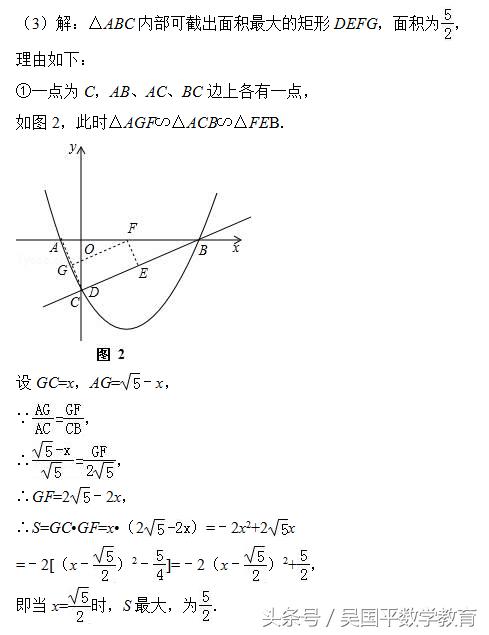
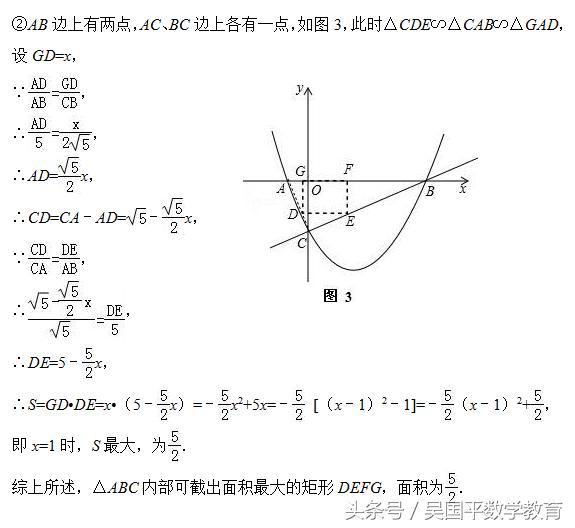
（3）△ABC内部能否截出面积最大的矩形DEFG？（顶点D、E、F、G在△ABC各边上）若能，求出最大面积；若不能，请说明理由．