高考数学：客观题讲解分析

典型例题分析1：

已知随机变量x服从正态分布N（3，σ2），且P（x≤4）=0.84，则P（2＜x＜4）=（ ）

A．0.84 B．0.68 C．0.32 D．0.16

解：∵P（x≤4）=0.84，

∴P（x＞4）=1﹣0.84=0.16

∴P（x＜2）=P（x＞4）=0.16，

∴P（2＜x＜4）=P（x≤4）﹣P（x＜2）=0.84﹣0.16=0.68

故选B．

考点分析：

正态分布曲线的特点及曲线所表示的意义．

题干分析：

根据对称性，由P（x≤4）=0.84的概率可求出P（x＜2）=P（x＞4）=0.16，即可求出P（2＜x＜4）．

典型例题分析2：

“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．其直观图如图，图中四边形是为体现其直观性所作的辅助线．当其主视图和侧视图完全相同时，它的俯视图可能是（ ）

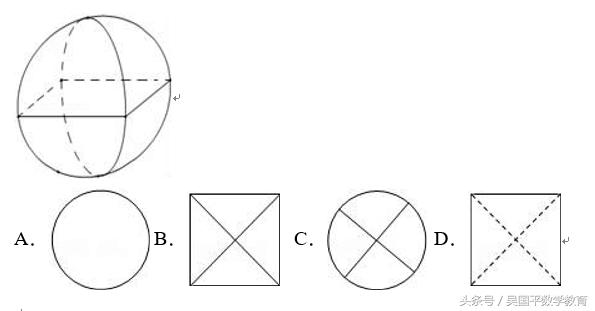
解：∵相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．

∴其正视图和侧视图是一个圆，

∵俯视图是从上向下看，相对的两个曲面在同一个圆柱的侧面上

∴俯视图是有2条对角线且为实线的正方形，

故选：B

考点分析：

简单空间图形的三视图．

题干分析：

相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．根据三视图看到方向，可以确定三个识图的形状，判断答案．

典型例题分析3：

已知集合A、B是非空集合且A⊆B，则下列说法错误的是（ ）

A．∃x0∈A，x0∈B B．∀x0∈A，x0∈B C．A∩B=A D．A∩（∁uB）≠∅

解：∵集合A、B是非空集合且A⊆B，

∴∃x0∈A，x0∈B；∀x0∈A，x0∈B；A∩B=A；A∩（∁uB）=∅．

因此A，B，C，正确，D错误．

故选：D．

考点分析：

特称命题．

题干分析：

利用元素与集合之间的关系、集合的运算性质即可判断出正误．

典型例题分析4：

执行如图所示的程序框图，若输出的S=63，则输入a的值可以是（ ）

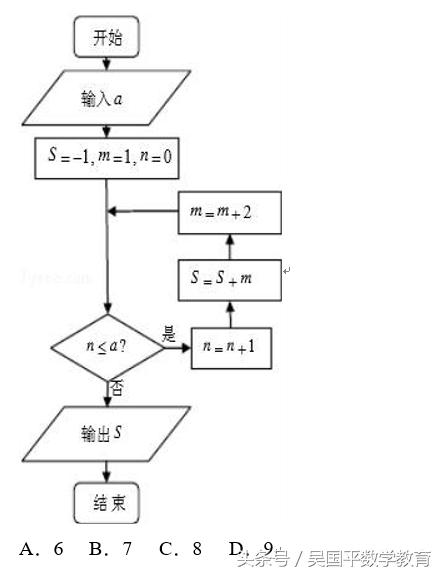
解：当m=1，n=0，S=﹣1时，不满足输出条件，故进行循环，执行完循环体后，n=1，s=0，m=3；

当m=3，n=1，S=0时，不满足输出条件，故进行循环，执行完循环体后，n=2，s=3，m=5；

当n=2，s=3，m=5时，不满足输出条件，故进行循环，执行完循环体后，n=3，s=8，m=7；

当n=3，s=8，m=7时，不满足输出条件，故进行循环，执行完循环体后，n=4，s=15，m=9；

当n=4，s=15，m=9时，不满足输出条件，故进行循环，执行完循环体后，n=5，s=24，m=11；

当n=5，s=24，m=11时，不满足输出条件，故进行循环，执行完循环体后，n=6，s=35，m=13；

当n=6，s=35，m=13时，不满足输出条件，故进行循环，执行完循环体后，n=7，s=48，m=15；

当n=7，s=48，m=15时，不满足输出条件，故进行循环，执行完循环体后，n=8，s=63，m=17；

若输出的S=63，则n≤7，故a=7，

故选：B．

考点分析：

程序框图．

题干分析：

由已知中的程序框图，可知：该程序的功能是计算并输出变量S的值，模拟程序的运行过程，分析出各变量的变化情况，可得答案．