九年级数学相似图形压轴题解析一例（4）

例题5、（2018年包头市中考数学第25题）如图，在矩形 ABCD 中 ， AB = 3 , BC = 5 , E 是 AD 上的一个动点 。

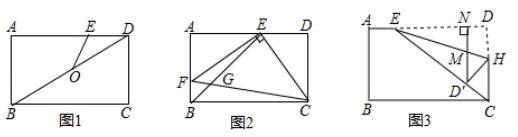
① 如图 1 、连接 BD ，O 是对角线 BD 的中点 ，连接 OE 。当 OE = DE 时，求 AE 的长 ；

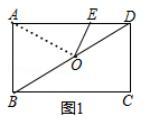
② 如图 2 、连接 BE 、EC ，过点 E 作 EF⊥EC 交 AB 于点 F ，连接 CF ，与 BE 交于点 G 。

当 BE 平分 ∠ABC 时 ，求 BG 的长 ；

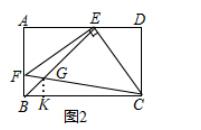
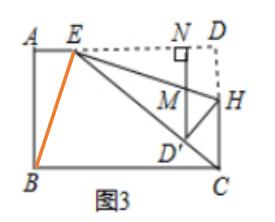
③ 如图 3 、连接 EC ，点 H 在 CD 上，将矩形 ABCD 沿直线 EH 折叠，折叠后点 D 落在 EC 上的点 D' 处，过点 D‘ 作 D‘N⊥AD 于 N ，与 EH 交于点 M ，且 AE = 1 。

（1）求 S△ED'M ：S△EMN 的值 ；

（2）连接 BE ，△D'MH 与 △CBE 是否相似？请说明理由 。

解题思路：

① 由△ABD 是直角三角形，O 是对角线 BD 的中点，可求出 OD = OB = OA ，在来证明 △ODE∽△ADO，即可求出 AE 的长；

② 先来证明 △AEF≌△DCE ，进而求出 BF = 1 ，过点 G 作 GK⊥BC 于点 K ，易证 △CKG∽△CBF ，通过方程设未知数和相似三角形的对应线段成比例，进而求出 BK = GK = 5/6 , 在等腰直角△BKG 中，用勾股定理即可得出结论；

③ （1）在 Rt△EDC 中，易求出 EC = 5 ，由 ED = ED' ,可求出 D'C = 1 ，根据勾股定理可求出 DH = 4/3，CH = 5/3 ,

再来证明 △EMN∽△EHD，则有 MN : HD = EM : EH ；△ED'M∽△ECH ，则有 D'M ：CH = EM ： EN ，

进而得出 D'M ：MN = CH : HD = 5/4 , 即可得出结论 ；

（2）先证明 ∠MD'H = ∠NED'（都和∠ED'N互余），进而得出 ∠MD'H = ∠ECB ，即可得出 D'M /CB = D'H/CE ，

即可证明 △D'MH 与 △CBE 是否相似 。

解答过程：

① 如图1，连接 OA ，在矩形 ABCD 中 ，CD= AB = 3 , AD = BC = 5 , ∠BAD = 90° ，

在 Rt△ABD 中 ，由勾股定理可得 ：BD = √34 。

∵ O 是 BD 的中点 ， ∴ OD = OB = OA = √34/2 ,

∴ ∠OAD = ∠ODA ，

∵ OE = DE , ∴ ∠EOD = ∠ODE ，

∴ △ODE∽△ADO ，

∴ DO/AD = DE/DO , 即 DO^2 = DE ▪ AD ,

设 AE = x ， 则 DE = 5 - x ,

∴ ( √34/2)^2 = 5 ▪ ( 5 - x ) ,

解得： x = 33/10 ,

∴ AE = 33/10 ;

② 如图2、过点 G 作 GK⊥BC ，垂足为点 K ，则 ∠GKB = 90° ，

∵ 在矩形 ABCD 中 ，BE 平分 ∠ABC ，

∴ ∠ABE = ∠CBE = 45° ，AD∥BC ，

∴ ∠AEB = ∠EBC ,

∴ ∠AEB = ∠ABE ，△AEB 为等腰直角三角形 ，

∴ AE = AB = CD = 3 ,

∵ EF⊥EC ，∴ ∠FEC = 90° ，

又 ∵ ∠AEF + ∠DEC = 180° - ∠FEC = 90° ，∠AEF + ∠AFE = 90° ，

∴ ∠AFE = ∠DEC ，

∵ ∠A = ∠D = 90° ， AE = DC ,

∴ △AEF≌△DCE （AAS）

∴ AF = DE = 2 , BF = AB - AF = 1 。

∵ ∠GKB = ∠ABC = 90° ， ∴ FB∥GK ，

∴ △CKG∽△CBF ，

∴ GK : BF = CK : CB ,

∵ ∠KBG = 45° ，∠GKB = 90° ，

∴ ∠BGK = 45° ，△BKG 是等腰直角三角形 。

设 BK = GK = y , 则 CK = 5 - y ,

∴ y : 1 = ( 5 - y ) : 5 , 解得 y = 5/6 ,

∴ BK = GK = 5/6 ,

∴ 在等腰直角 △BKG中 ，BG = √2 BK = 5√2/6 。

③ (1) 在矩形 ABCD 中 ， ∠D = 90° ，

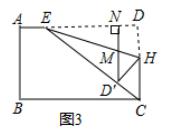
∵ AE = 1 , AD = 5 , ∴ DE = 4 ,

∵ DC = 3 , ∴ 在 Rt△EDC 中，EC = 5 。

由折叠可知：ED' = ED = 4 , D'H = DH , ∠ED'H = ∠D ，

∴ D'C = 1 ，

设 D'H = DH = z , 则有 HC = 3 - z ，

在 Rt△HD'C 中，由勾股定理可得 ：（3 - z）^2 = 1^2 + z^2 ,

∴ 解得 z = 4/3 ，

∴ DH = 4/3 , CH = 5/3 。

∵ D'N⊥AD ，∴ ∠AND' = ∠D = 90° ，

∴ D'N∥DC ，

∴ △EMN∽△EHD ，△ED'M∽△ECH ，

∴ MN/HD = EM/EH , D'M/CH = EM/EH ,

∴ MN/HD = D'M/CH ,

∴ D'M/MN = CH/HD = 5/4 ,

∴ S△ED'M ：S△EMN = 5/4 ；

(2) 相似。

理由：由折叠的性质可知，∠EHD' = ∠EHD ，∠ED'H = ∠D = 90° ，

∴ ∠MD'H + ∠ED'N = 90° ，

∵ ∠END' = 90° ， ∴ ∠ED'N + ∠NED' = 90° ，

∴ ∠MD'H = ∠NED' ,

∵ D'N∥DC ， ∴ ∠EHD = ∠D'MH ，

∴ ∠EHD' = ∠D'MH ,

∴ D'M = D'H ,

又 ∵ AD∥DC ， ∴ ∠NED' = ∠ECB ，

∴ ∠MD'H = ∠ECB ，

∵ CE = CB = 5 ,

∴ D'M/CB = D'N/CE ,

∴ △D'MH ∽ △CBE 。

评注：此题是相似形综合题，主要考查了矩形的性质，相似三角形的判定和性质，勾股定理，角平分线的定义，及列方程解未知数等知识，熟练掌握判定两三角形相似的方法是解本题的关键。