中考数学压轴题直线旋转就这么想

【思路分析】

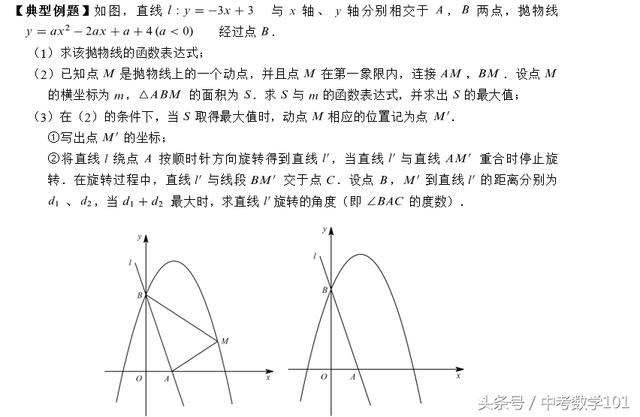
（1）第1问直线l与x、y轴相较于A、B两点，分别令y=0、x=0可以求出点A、B的坐标，根6据待定系数法，就可以求出抛物线的解析式；学生在答题时注意细心即可！

（2）第2问设出点M的坐标，连接OM，则三角形ABM的面积等于四边形OAMB的面积减去三角形ABO的面积，由此等量关系式可以求出S与m的函数解析式，这是S关于m的二次函数表达式，然后根据二次函数的图像与性质求出最大值；

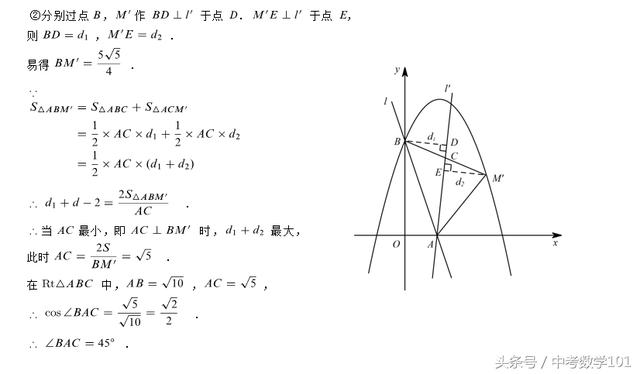
（3）第3问要注意审题，这是在（2）的条件下进行求解的，这是本题的易错点！①在（2）的条件下，当S有最大值的时候，动点M相应的位置记为M’，此时点M’的横坐标是m=2.5，代入二次函数的解析式即可求出纵坐标的值；②作BD垂直l’，M’E垂直l’，根据三角形ABM’的面积可以求出d1与d2的和，因此，当AC最小的时候，d1与d2的和最大，此时可知AC垂直BM’，求得AC等于根号五，在直角三角形ABC中，解直角三角形求出直线l’旋转的角度即可；