中考二次函数压轴题抛物线旋转问题分析

【思路分析】

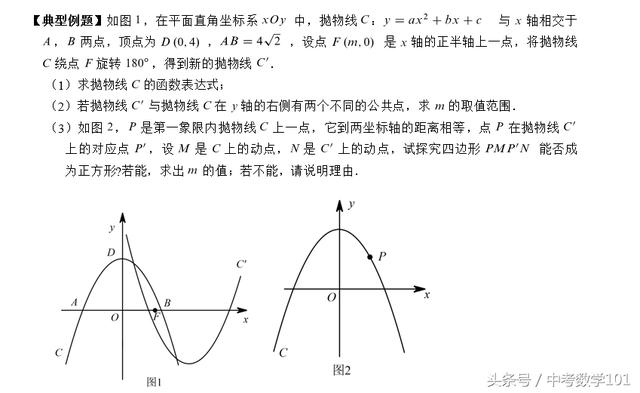
（1）第1问属于基础题，由A、B、D三点的坐标，根据待定系数法，可求出抛物线的解析式，注意计算不要出错即可；

（2）第2问将抛物线C绕着点F旋转180°后，得到新的抛物线C’，则抛物线C的顶点D（0,4）绕点F旋转180°后得到的对应点D’（2m,-4）为新的抛物线C’的顶点，因此可以设出C’的顶点式，然后结合图形，从抛物线C’与抛物线C在y轴右侧有两个不同的公共点时的两个临界点，一是抛物线C’经过点D，而是点B、F重合；数形结合，从草图分析得出结论；

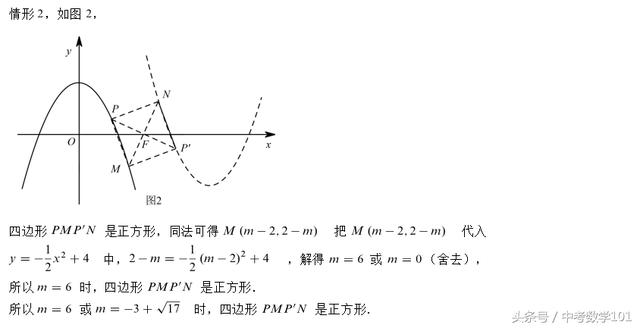
（3）第3问先求出点P的坐标（2,2），四边形PMP’N是正方形时，只有线段PP’是正方形的对角线这一种情况，此时画出简图，然后分类讨论。