初中几何题中弦切角应该如何分析？

本次的三道例题皆是关于含有圆的弦切角的几何经典例题。在初中的几何证明里，有圆的几何题往往会很复杂，因为其在证明过程中多少会牵涉到其他几何图形，诸如三角形、四边形等。

利用基本图形分析法，首先就是要明白

最关键的第一步：拿到问题后是怎么想的？

所以一起看一下在拿到关于含有圆的弦切角的几何经典例题时应该如何分析吧

当几何问题中出现圆的切线或圆的半径的垂线时，就应想到要应用弦切角的基本图形进行证明。

如出现了圆的切线，但未出现弦切角时，首先应添加过切点的弦或过切点的直径(半径)，然后在必要时还应添加这个弦切角所夹的弧所对的四周角，从而就可以应用弦切角的基本图形的性质完成分析。

如出现的是四的半径的垂线，则应添加过半径外端的四的切线，然后再应用弦切角的基本图形和平行线的基本图形的性质完成分析。

当几何问题中出现了相切圆的问题时，就应想到要将问题转化到一个圆中的问题来进行分析和讨论，转化的方法是添加过切点的两圆的公切线。接下来就可以分别在每一个圆中应用弦切角的基本图形的性质来完成分析。

例64如图4-175已知：⊙O、⊙O′外切于P，AD是⊙O、⊙O′的外公切线，切点是A、D，AB是直径，BC与⊙O′相切于C。求证：BC=BA

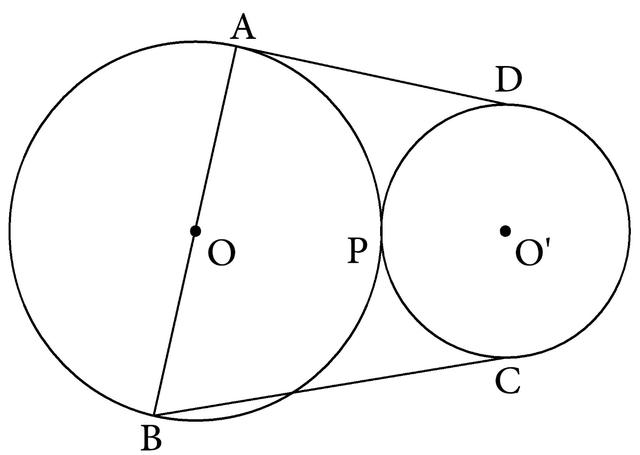
图4-175

分析：由于⊙O、⊙O′外切于P，所以可添加过切点的公切线，把问题转化成为一个圆中的弦切角的基本图形问题来分析。

于是过P作⊙O、⊙O的内公切线交AD于E（如图4-176）。这样，在⊙O中就出现EA、EP都与⊙O相切，切点分别是A、P，所以EP=EA，同时它们也是两条具有公共端点的相等线段，就可组成一个等腰三角形，但这个等腰三角形只有两条腰而没有底边，故联结PA（如图4-176），可得∠EAP和∠EPA这两个弦切角相等。根据同样的道理，在⊙O′中，联结PD（如图4-176）后，也可得EP=ED，∠EDP=∠EPD。由于这四个角之和等于180°，所以∠APD=∠APE+∠DPE=90°

由条件AB是⊙O的直径，所以可应用半圆上的圆周角的基本图形的性质进行证明，现在图形中是有直径，有半圆上的点P，而没有圆周角，故联结BP（如图4-176），就可得∠APB=90°，于是∠APD+∠APB=180°，B、P、D成一直线，又因为DA与⊙O相切于A，而AB是⊙O的直径，所以∠DAB=90°。这样AP就成为直角△ABD的斜边上的高，于是就可应用直角三角形斜边上的高的基本图形的性质进行证明。由于结论中出现的线段是BA，所以应用射影定理时，可选取BA²=BP·BD，从而问题转化为要证明BC²也等于BP·BD。但现在BC与⊙O′相切于C，BPD是割线，所以应用切割线定理就可以证明上述性质。

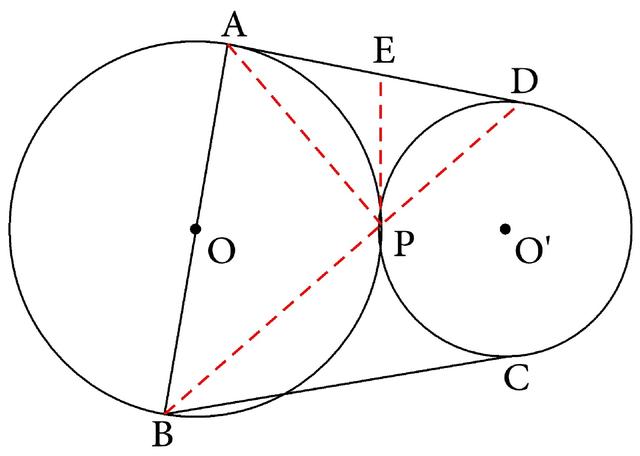
图4-176

例65如图4-177，已知：⊙O、⊙O′外切于A，外公切线BC与⊙O、⊙O′相切于B、C。求证：以BC为直径的圆与O0′相切

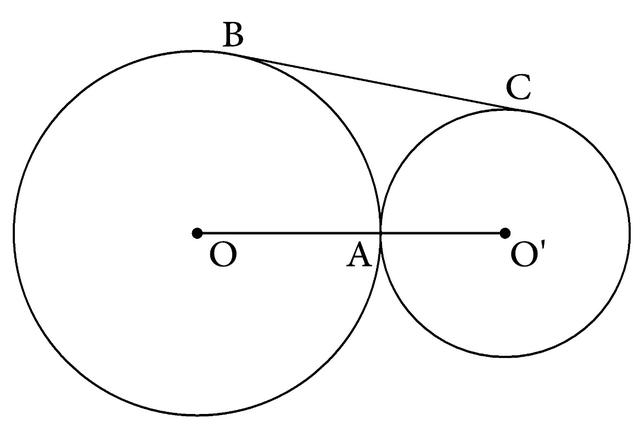
图4-177

分析：由于⊙O与⊙O′外切于A，是一个两圆相切的问题，所以可通过添加过切点的公切线，将问题转化成每一个圆中的切线问题来解决。

于是过A作⊙O、⊙O′的内公切线交BC于D（如图4-178），那么由DB、DA分别与⊙O相切于B、A，应用切线长定理即可得DB=DA，根据同样的道理还可得DA=DC。这样D就成为BC的中点，所以以BC为直径所作的圆必定过点A。这样问题就只要证这个圆与OO′相切于A。但DA是这个圆的半径，且OO′⊥DA，所以OO′必定与这个以BC为直径的圆相切于点A。

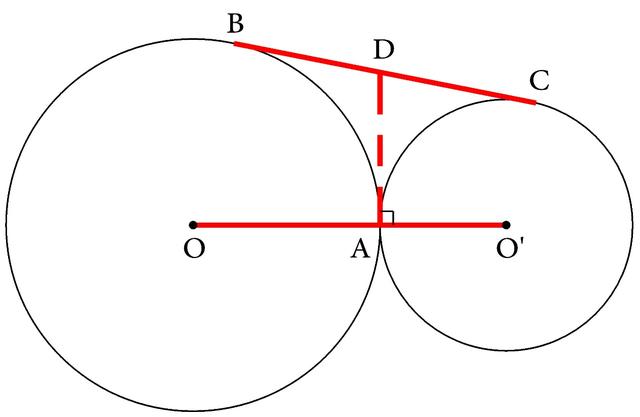
图4-178

例66如图4-179，已知：⊙O、⊙O′外切于A，外公切线BC与⊙O、⊙O′相切于B、C。求证：以OO′为直径的圆与BC相切。

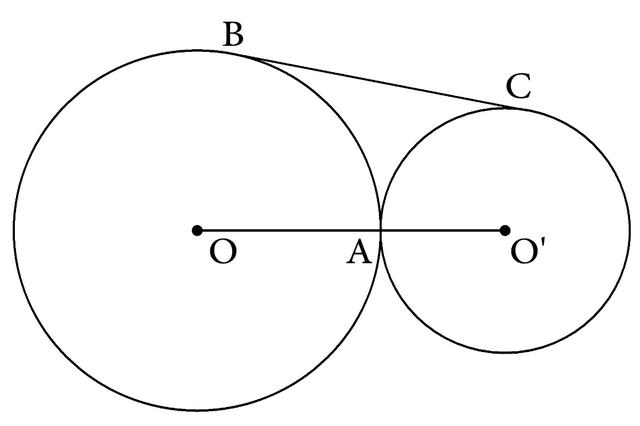
图4-179

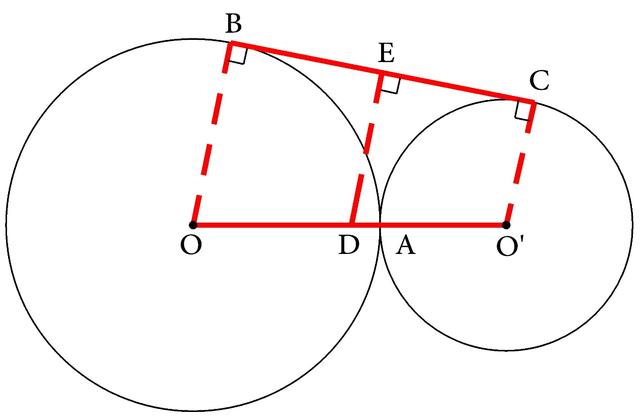
分析：以OO′为直径的圆也就是以OO′的中点为圆心、以1/2OO'的长为半径所作的圆。于是取OO′的中点D，然后应证以D为圆心、以DO长为半径所作的圆必定和BC相切，也就是证D到BC的距离就等于DO。于是过D作DE⊥BC，垂足是E（如图4-180），问题就应证DE=DO=DO′。

又因为BC是两圆的外公切线，所以BC也可以看作是每一个圆的切线，于是又可应用弦切角的基本图形的性质进行证明，从而联结OB和O′C（如图4-180），就可得∠OBC=∠O′CB=90°，OB∥DE∥O′C，于是E就是BC的中点，DE就是梯形OO′CB的一条中位线。而应用梯形中位线的性质可得DE=（OB+O′C）/2=（R+r）/2，而DO=DO=OO′/2=（R+r）/2，所以就有DO=DO′=DE，从而就可完成分析。