高中数学直线与方程知识点总结
1.直线的倾斜角
(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为0°.
(2)范围:直线l倾斜角的范围是[0°,180°).
2.斜率公式
(1)若直线l的倾斜角α≠90°,则斜率k=tan_α.
(2)P1(x1,y1),P2(x2,y2)在直线l上且x1≠x2,则l的斜率k=(y2-y1)/(x2-x1).
3.直线方程的五种形式

题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)根据直线的倾斜角的大小不能确定直线的位置.(√)
(2)坐标平面内的任何一条直线均有倾斜角与斜率.(×)
(3)直线的倾斜角越大,其斜率就越大.(×)
(4)若直线的斜率为tanα,则其倾斜角为α.(×)
(5)斜率相等的两直线的倾斜角不一定相等.(×)
(6)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.(√)
2.若过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4
C.1或3 D.1或4


综上可知,直线m的方程为x-2y+2=0或x=2.
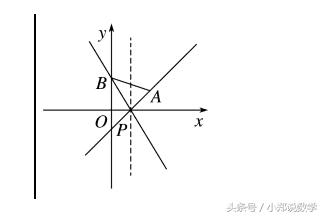
(2)直线l过点P(1,0),且与以A(2,1),B(0,√3)为端点的线段有公共点,则直线l斜率的取值范围为___________________.
答案(-∞,-]∪[1,+∞)
解析如图
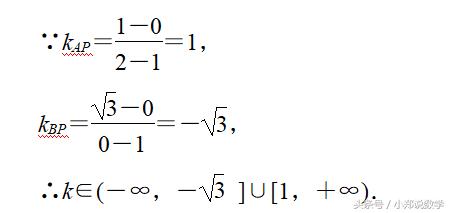
直线方程的综合应用



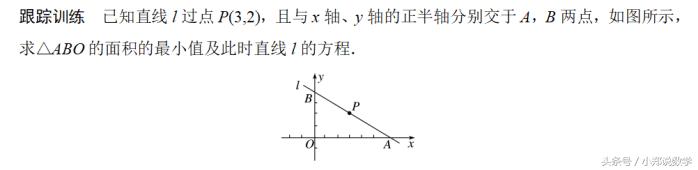

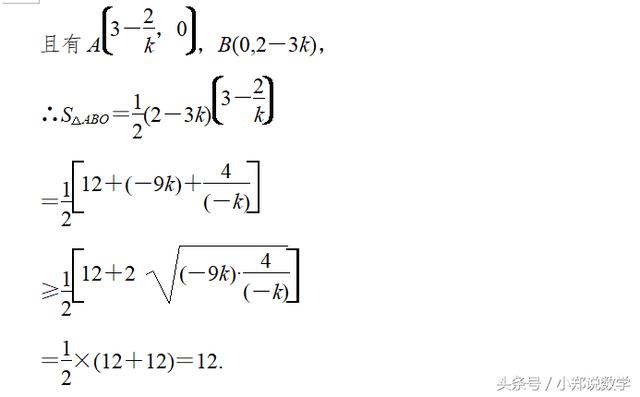

课时作业:

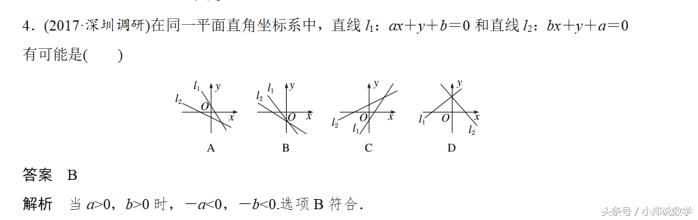







 加载中,请稍侯......
加载中,请稍侯......
精彩评论