高中数学一元二次不等式与二元一次不等式组的解法

一、一元二次不等式与分式不等式

1、一元二次不等式的解集端点→一元二次方程的解→二次函数的零点。

2、解一元二次不等式的步骤：

二次项系数化为正→因式分解（求根）→判断符号（大于0，两根之外，小于0，两根之外）

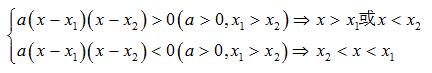
3、分式不等式：

转化成整式不等式求解

二、二元一次不等式解法

1、可行域的判断依据：

y 的系数 by 与不等号 ，同号，直线上方；异号，直线下方 。

2、目标函数平移规律：

y 的系数 b 为正，往上平移变大； y 的系数 b 为负，往上平移变小

三、典型例题

1、解含参一元二次不等式与分式不等式

例题1：已知 0 < a < 1，则关于 x 的不等式 （x - a）（x - 1/a）> 0 的解集为 ？

解：根据不等式的性质可得

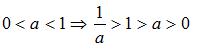
故而可得解集为

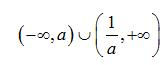
变式：

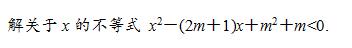
解析：将不等式因式分解可得

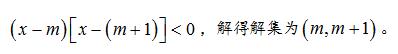
例题2：若 a < 0，则不等式

解析：将不等式化简可得

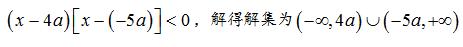
2、不等式中的参数求解

例题3：函数

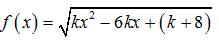
的定义域为 R，则实数 k 的取值范围为 ( )

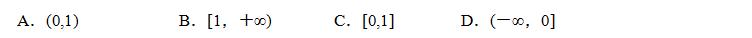
解析：函数的定义域为 R，故而可得

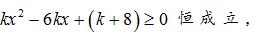
故而

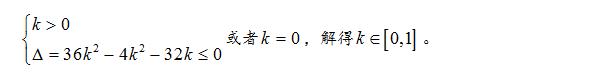
变式：若不等式

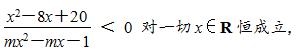
则实数m的取值范围为________。

解析：化简可得

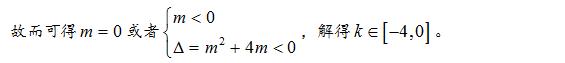
例题4：设不等式 mx^2－2x－m＋1＜0 对于满足 |m| ≤ 2的一切 m 的值都成立，求 x 的取值范围 。

解析：将不等式化简可得

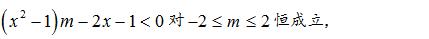
故而将 m 当作自变量，这是一个一次函数，故而可得

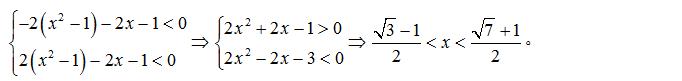
3、二元一次不等式组的基础解法

例题5：（2017年课标1卷13题）设 x，y 满足约束条件

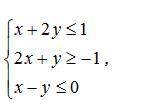
则 z = 3x - 2y 的最小值为 ________。

解析：根据约束条件可画出可行域如图所示，

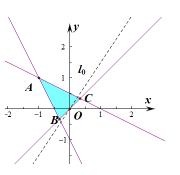
y 的系数为负，故而可得当初始函数平移经过点 A 时函数取最小值，联立

4、含参二元一次不等式组的解法

例题6：已知 x , y 满足约束条件

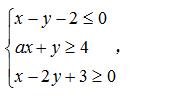
目标函数 z = 2x - 3y 的最大值是2，则实数 a = （ A ）

解析：根据约束条件可以发现，可行域必然在直线 x - y - 2 = 0 的上方和直线 x - 2y + 3 = 0 的下方，直线 y = 4 - ax 是恒过点

（0 , 4）的一条直线。

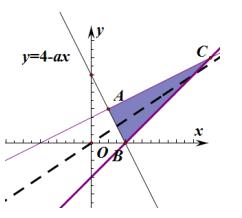
故而要使得存在可行域，直线 y = 4 - ax 必须顺时针旋转，目标函数 z = 2x - 3y 的系数为负，故而向下平移的过程中不断变大，因此可得目标函数在点 B 处取到最大值。联立方程

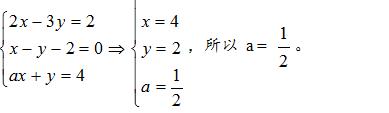
例题7：设实数 x ，y 满足约束条件

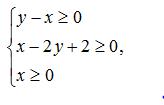
若目标函数 z = mx + y ( m > 0 ) 的最大值为6，则 m 的值为（A ）

解析：根据约束条件可以画出可行域如图所示，

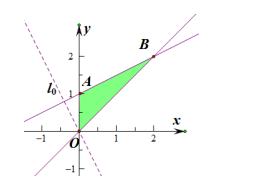
目标函数 z = mx + y 的初始直线斜率为负，系数为正，故而可得无论直线如何旋转，都将在点 B 处取最大值。

联立方程

解题思路：

此类问题包含两种形式，一种是约束条件中含有参数，一种是目标函数中含有参数。

两种问题都涉及到分类讨论和函数的旋转。

① 约束条件含参：影响斜率，对直线进行旋转；影响截距，对直线进行平移。

② 目标函数含参：对参数进行正负的讨论，注意与可行域中的约束条件进行对比讨论。