九年级数学二次函数压轴题解析一例（3）

例题3、如图，在平面直角坐标系中，已知抛物线

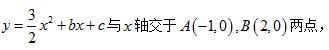
与 y 轴交于点 C 。

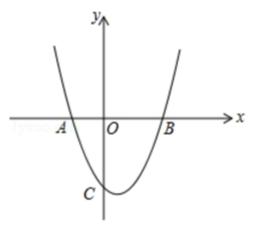
（1）求该抛物线的解析式；

（2）直线 y = -x + n 与该抛物线在第四象限内交于点 D ，与线段 BC 交于点 E ，与 x 轴交于点 F ，且 BE = 4EC 。

① 求 n 的值；

② 连接 AC , CD ，线段 AC 与线段 DF 交于点 G ，△AGG 与 △CGD 是否全等？请说明理由；

（3）直线 y = m ( m > 0 ) 与该抛物线的交点为 M , N （点 M 在点 N 的左侧），点 M 关于 y 轴的对称点为点 M' ，点 H 的坐标为（1 ，0）.若四边形 OM'NH 的面积为 5/3 ， 求点 H 到 OM' 的距离 d 的值。

试题解析：

（1）∵ 抛物线 y = 3/2 x^2 + bx + c 与 x 轴交于 A（-1,0），B（2,0）两点，

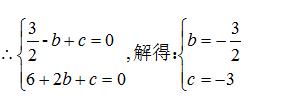
∴ 该抛物线的解析式 y = 3/2 x^2 - 3/2 x - 3 ；

（2）① 如图，过点 E 作 EE'⊥x 轴于 E‘ ，则 EE'∥OC ，

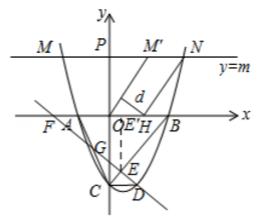
∴ BE' : OE' = BE : CE , ∵ BE = 4EC , ∴ BE' = 4OE' ,

设点 E 的坐标为 （x , y），则 OE' = x , BE' = 4x ,

∵ B（2,0），∴ OB = 2 , 即 x + 4x = 2 ,

∴ x = 2/5 ,

∵ 抛物线 y = 3/2 x^2 - 3/2 x - 3 与 y 轴交于点 C ，

∴ C（0，-3），设直线 BC 的解析式为 y = kx + b' ,

∵ B（2,0）, C（0，-3）,

∴ 2k + b' = 0 , -3 = b' . 解得：k = 3/2 , b' = -3 .

∴ 直线 BC 的解析式为 y = 3/2 x - 3 ,

当 x = 2/5 时 ，y = -12/5 ,

∴ E（2/5 ，-12/5），把 E点坐标带入直线 y = -x + n ，

可得 -12/5 = -2/5 + n , 解得 n = -2 ；

② △AGF 与 △CGD 全等 。理由如下：

∵ 直线 EF 的解析式为 y = -x - 2 ,

∴ 当 y = 0 时，x = -2 , ∴ F（-2,0）, OF = 2 ,

∵ A（-1,0）， ∴ OA = 1

∴ AF = 2 - 1 = 1 ，

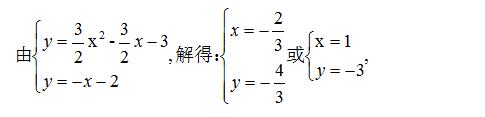
∵ 点 D 在第四象限，∴ 点 D 的坐标为 （1，-3），

∵ 点 C 坐标为 （0，-3），∴ CD∥ x 轴 ， CD = 1 ，

∴ ∠AFG = ∠CDG ，∠FAG = ∠DCG ，CD = AF，

∴ △AGF ≌ △CGD 。

（3）∵ 抛物线的对称轴为 x = -b/2a = 1/2 , 直线 y = m ( m > 0 ) 与该抛物线的交点为 M , N ,

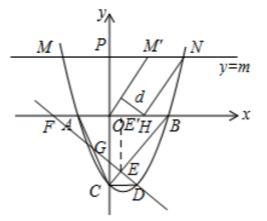
∴ 点 M , N 关于直线 x = 1/2 对称 ，

设 N（t , m）, 则 M（1 - t , m）,

∵ 点 M 关于 y 轴的对称点为点 M' ,

∴ M'（t - 1 , m）,

∴ 点 M' 在直线 y = m 上 ，

∴ M'N ∥x轴 ，∴ M'N = t - ( t - 1 ) = 1 ,

∴ OH = 1 = M'N , 四边形 OM'NH 是平行四边形 ，

设直线 y = m 与 y 轴交于点 P ，

∵ 四边形 OM'NH 的面积为 5/3 ，

∴ OH × OP = 1 × m = 5/3 ， 即 m = 5/3 ，

∴ OP = 5/3 ，

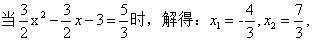
∴ 点 M 的坐标为 （-4/3 , 5/3）, M'（4/3,5/3）, 即 PM' = 4/3 ,

∴ 在 Rt△OPM' 中 ，

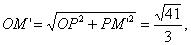
∵ 四边形 OM'NH 的面积为 5/3 ，

∴ OM' × d = 5/3 ,

∴ d = 5√41 / 41 。