高中数学解析几何之椭圆性质及例题

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

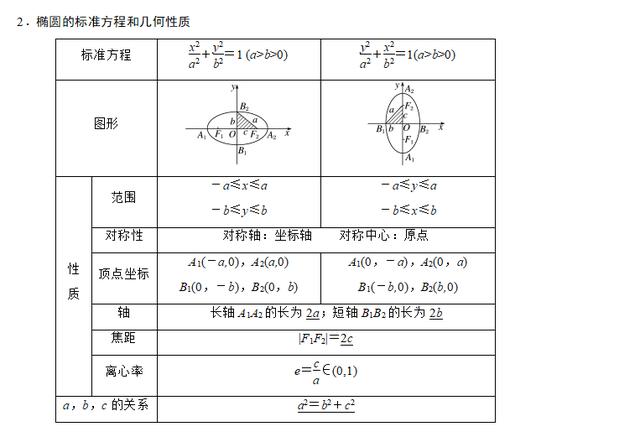
1．椭圆的概念

平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．

集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a>0，c>0，且a，c为常数：

(1)若a>c，则集合P为椭圆；

(2)若a＝c，则集合P为线段；

(3)若a<c，则集合P为空集．

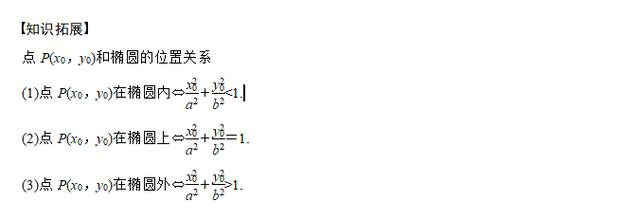
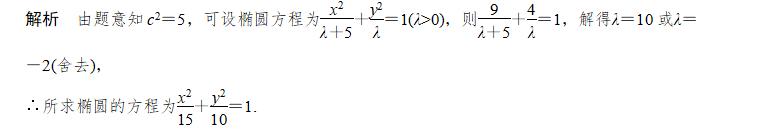
第1课时　椭圆及其性质

思维提升：

椭圆定义的应用技巧

(1)椭圆定义的应用主要有：求椭圆的标准方程，求焦点三角形的周长、面积及弦长、最值和离心率等．

(2)通常定义和余弦定理结合使用，求解关于焦点三角形的周长和面积问题．

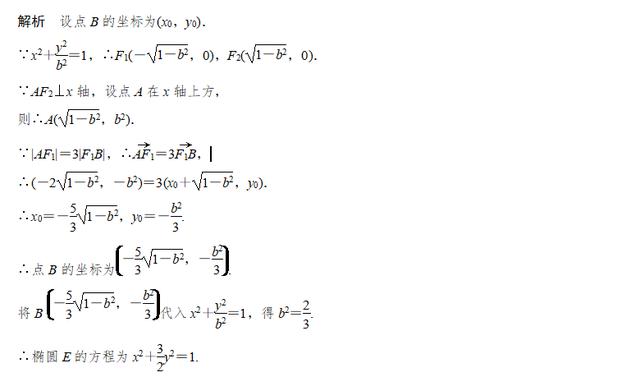
思维提升：

(1)利用椭圆几何性质的注意点及技巧

①注意椭圆几何性质中的不等关系

在求与椭圆有关的一些范围问题时，经常用到x，y的范围，离心率的范围等不等关系．

②利用椭圆几何性质的技巧

求解与椭圆几何性质有关的问题时，理清顶点、焦点、长轴、短轴等基本量的内在联系．

(2)求椭圆的离心率问题的一般思路

求椭圆的离心率或其范围时，一般是依据题设得出一个关于a，b，c的等式或不等式，即可得离心率或离心率的范围．