中考二次函数压轴题函数动点与四边形周长最小值

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

【思路分析】

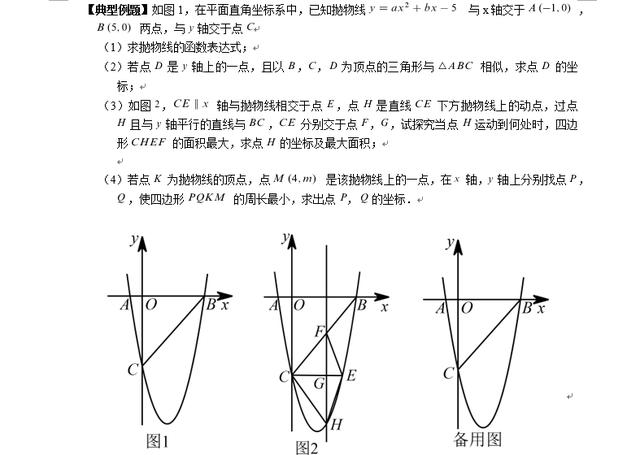
（1）二次函数压轴题第1问常规套路，根据待定系数法可求出二次函数的解析式，注意不要粗心即可；

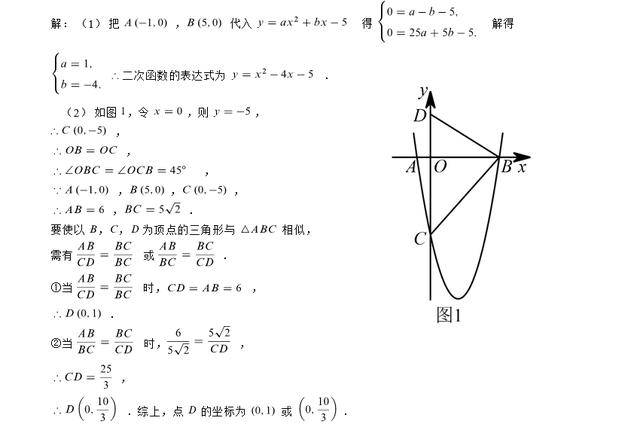
（2）第2问首先从图形直观来说，三角形ABC是一个锐角三角形，并且角ABC等于45°，角ABC两边长分别为AB=6，BC由勾股定理可求得长度是五倍根号二。其次，点D是y轴上的一个动点，以B、C、D为顶点的三角形与三角形ABC相似，那么点D的位置只能出现在点C上方的y轴上（否则角BCD就会等于135°），此时角BCD等于45°，这样我们就找出了两个三角形的一对对应角相等，假设这个角的两边对应成比例，那么这两个三角形必然相似，由于确定的对应顶点，因此需要分两种情况分别列比例式，在从中解出点D的坐标；

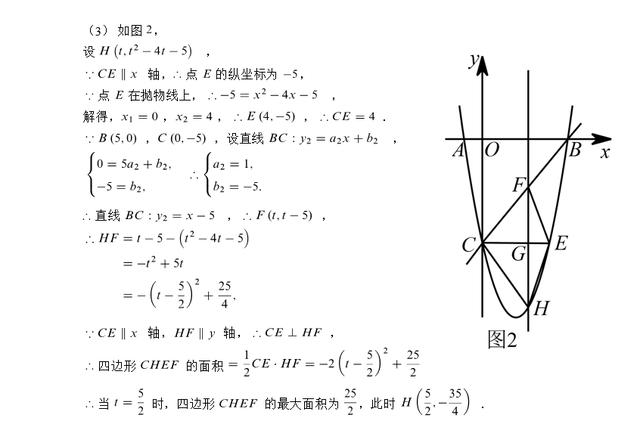
（3）第3问中，所求四边形是一个对角线互相垂直的四边形，因此它的面积是对角线乘积的一半，只要我们先求出直线BC的解析式，那么我们就可以进一步表示出四边形CHEF的面积的函数关系式，再根据二次函数的图像与性质，可以求出四边形CHEF的面积的最大值；

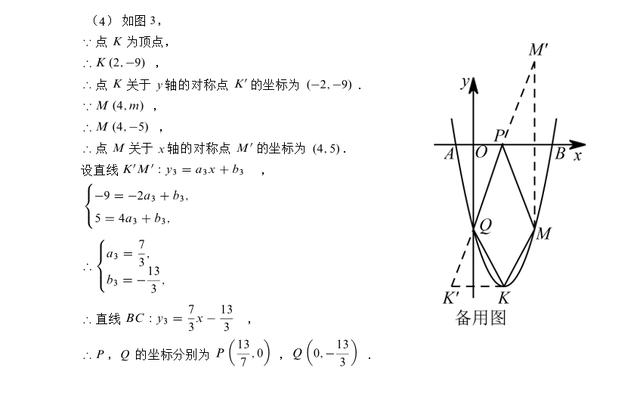
（4）由抛物线解析式可知顶点坐标为K（2，-9），点M的坐标为（4，-5），作点K关于y轴的对称点K’（-2，-9），作点M关于x轴的对称点M’（4，5），联结M’K’分别交x轴于点P，交y轴于点Q，则M’K’+MK的长度是四边形PQKM的最小周长，在根据待定系数法可求直线M’K’解析式，根据坐标轴上的点坐标特征求出点P、Q的坐标。