中考数学压轴题二次函数中动点与菱形存在性问题

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

【思路探究】

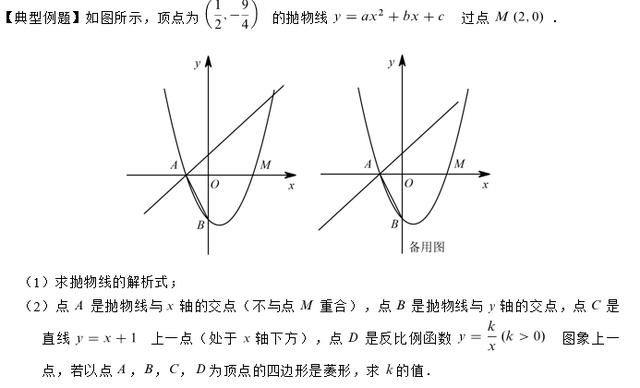
（1）二次函数综合题的第1问通常都是求函数解析式，或者求抛物线与坐标轴交点的坐标、顶点坐标等，属于基础题难度不大，在第1问中根据已知顶点，可设抛物线的顶点式y=a(x-h)²+k，然后代入点M（2,0）以及顶点的坐标，求出参数a的值即可。

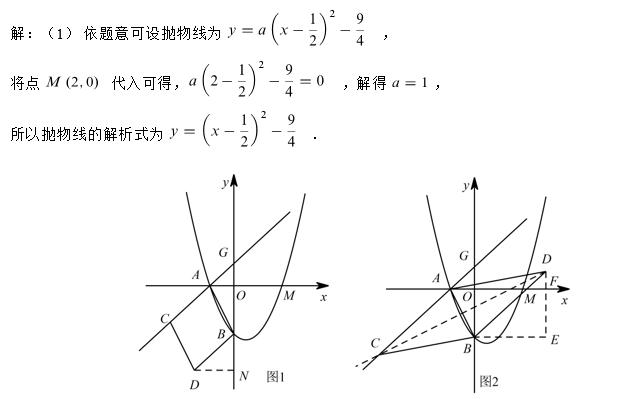
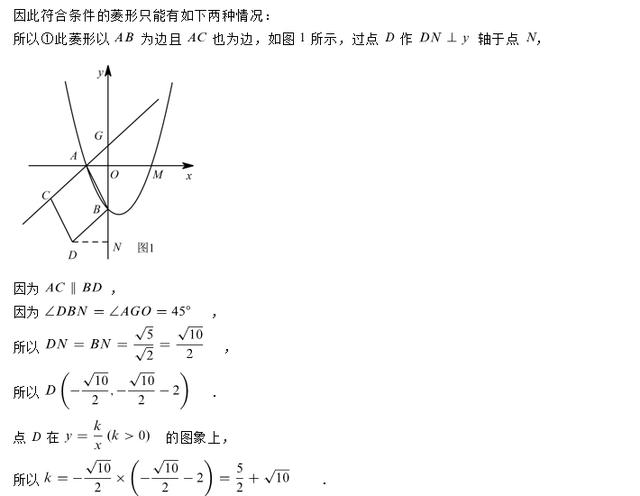
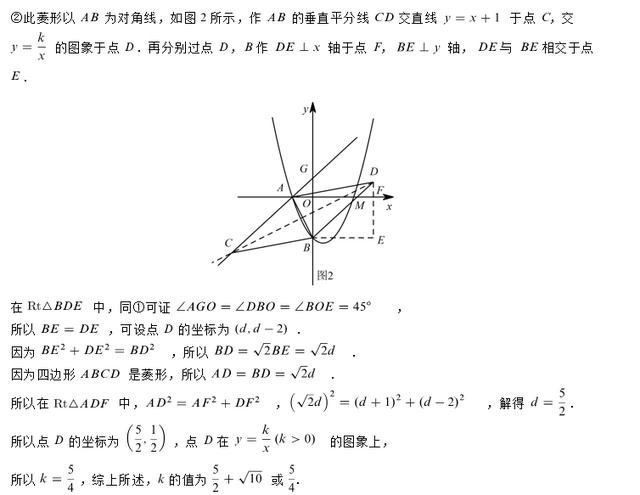
（2）第2问是本题的难点，难就难在要根据题意画出符合条件的菱形，其次在综合性问题当中容易出现考虑问题不全面而导致漏解，这是本小问最容易犯错的地方。根据抛物线的图像可知A、B两点的坐标是不变的，由已知条件分析可知点C在直线上且在x轴下方，点D在一三象限的反比例函数的图像上，因此四个点中有两个点是确定的，另外两个点有限制条件，因此构成菱形ABCD的四个点的位置顺序是需要分类讨论的，结合图形画出草图分析，分别以AB、AC为一组邻边相等或以AB为对角线进行求解。

（3）本题主要考察的是二次函数的综合应用，主要涉及了待定系数法求反比例、二次函数解析式、勾股定理、等腰三角形的性质、菱形的性质等相关知识点，运用分类讨论的思想，由题意画出草图分析是解答本题难点的关键。