中考二次函数压轴题平行四边形存在性问题

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

【思路探究】

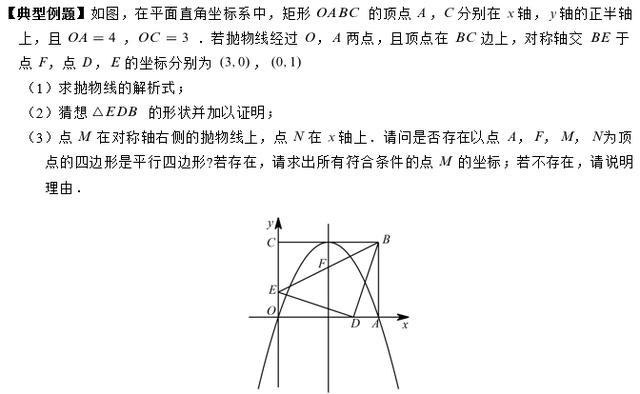
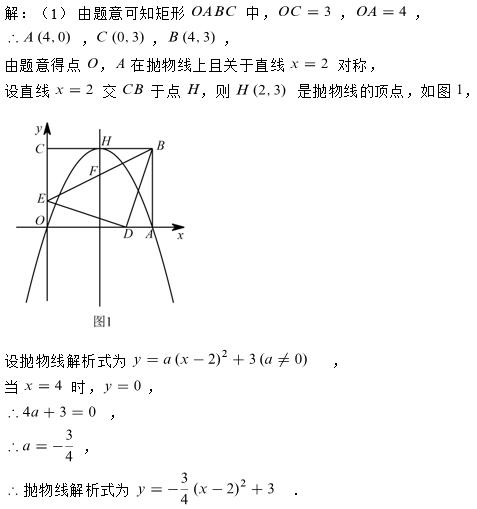
（1）二次函数压轴题的第1小问，通常都是考察二次函数的基础知识，一般以待定系数法求解析式为主，或者已知函数的解析式求抛物线的顶点坐标、图像与坐标轴的交点坐标等。本小问可以利用顶点式，也可以根据A（4,0）、O（0，0）设出交点式y=ax(x-4)，再将顶点坐标（2，3）代入求出参数a的值。

（2）第2小问如何合理猜想呢？要知道中考试卷当中图形的准确性，为我们提供了思考的方向，直接可以通过图形直观看出结论，大胆猜想三角形EDB是一个等腰直角三角形。有了猜想之后，猜想的结论正确与否，需要我们经过推理说明。我们只需要利用两点间距离公式，由B、D、E三个点的坐标分别求出DE、BD和BE的长度，再通过勾股定理的逆定理验证我们的猜想；或者证明三角形EOD和三角形DAB全等，再证明∠EBD是90°也可以。研究数学问题，需要大胆猜想，没有猜想就没有新的发现，猜想的依据也需要解题经验。思路整理清楚后，我们只需要将解题的格式、推理论证的过程及条理性表达清楚即可，目的就是考察数学思维严谨性。

（3）第3小问是本题的难点，虽然限制了点M在对称轴的右侧抛物线上，但是还有会有多种可能情况，一般情况下，学生都是画出平行四边形去分析的，往往存在考虑问题不周全而导致漏解的情况。而以点A、F、M、N为顶点的四边形是平行四边形，这四个点当中，点A、F是已知点，点M、N是加了限制条件的动点，同时题目没有具体交代四个点的位置顺序，因此需要进行分类讨论，即以AF为边或以AF为对角线，进而通过计算求得M的坐标。具体过程如下：