“两类压轴题”的抢分攻略，你学会了吗？

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

策略

1

缺步解答

能解多少算多少

如果遇到一个很困难的问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败．特别是那些解题层次明显的题目，或者是已经程序化了的方法，每进行一步得分点的演算都可以得分，最后结论虽然未得出，但分数却已过半，这叫“大题巧拿分”．

例题1

解答

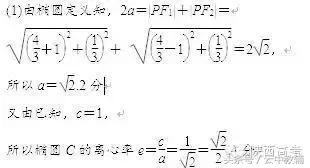
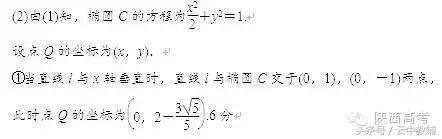
(1)本题第(1)问为已知椭圆标准方程求椭圆的离心率问题，属于容易题．

(2)本题的难点在于第(2)问中确定轨迹方程及方程中各变量的取值范围，本题有一定的难度，要想拿到全分很难，这就应该学会缺步解答．

抢分有招

首先，解决直线与圆锥曲线的位置关系问题时，若需要设直线方程，应考虑直线的斜率是否存在，因此当直线l的斜率不存在时，求出点Q的坐标为

.这是每位考生都应该能做到的．

其次，联立直线方程与椭圆方程并设出M，N，Q的坐标，通过

，得到

，然后由x1＋x2及x1x2联想一元二次方程根与系数的关系，将问题解决到

是完全可以做到的，到此已经可以得到9分．

另外，考虑到点Q在直线l上，将点Q坐标代入所设直线方程就能得到10(y－2)2－3x2＝18，到此便可以得到10分．

到此不能继续往下解时，我们也已经得到绝大部分分数了．

策略

2

跳步解答

左右逢源，会做哪问做哪问

解题过程中卡在某一过渡环节上是常见的．这时，我们可以先承认中间结论，往后推，看能否得到结论．若题目有两问，第(1)问想不出来，可把第(1)问当作“已知”，先做第(2)问，跳一步解答．

例题2

解答

抢分有招

第(1)问可利用函数的单调性及零点存在性定理较简单解决，但第(2)问较麻烦，很多同学不会做或耽误较长时间，从而延误了第(3)问的解答．事实上，由题意可知，第(3)问的解答与第(2)问没有任何关系，但与第(1)问是相关的，且非常容易解答，因此我们可跨过第(2)问，先解决第(3)问，从而增大了本题的得分率，这是解决此类题的上策之举．

策略

3

逆向解答

逆水行舟，往往也能解决问题

对一个问题正面思考发生思维受阻时，用逆向思维的方法去探求新的解题途径，往往能得到突破性的进展．顺向推有困难就逆推，直接证有困难就反证．

例题3

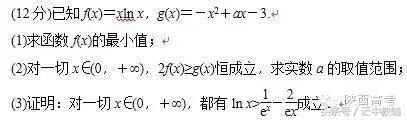
解答

抢分有招

解答本题第(3)问利用了逆向解答，把不等式

巧妙地转化为

，不等式左边是f(x)，右边看作一个新的函数

m(x)，只需说明f(x)min>m(x)max即可．

策略

4

退步解答

以退为进，列出相关内容也能得分

“以退求进”是一个重要的解题策略．对于一个较一般的问题，如果你一时不能解决所提出的问题，那么，你可以从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从参变量退到常量，从较强的结论退到较弱的结论．总之，退到一个你能够解决的问题，通过对“特殊”的思考与解决，启发思维，达到对“一般”的解决．

例题4

解答

抢分有招

在求解第(2)问时可采用退步解答，若不能正确判断其结论也应说明直线是否存在，同时应对直线垂直于x轴时给予说明，这就是所谓的从一般到特殊．