初中数学典型习题讲解

1、二次函数y=1/6(x+2√3)²的图像的顶点为A，与y轴交于点B，以AB为边在第二象限内作等边三角形ABC．

（1）求直线AB的表达式和点C的坐标． （2）点(m，1)在第二象限，且△ABM的面积等于△ABC的面积，求点M的坐标． （3）以x轴上的点N为圆心，1为半径的圆，与以点C为圆心，CM的长为半径的圆相切，直接写出点N的坐标．

解：

（1）二次函数y=1/6(x+2√3)²的图像的顶点A(-2√3，0)，与y轴的交点B(0，2)，

设直线AB的表达式为y=kx+b(k≠0)，

可求得 k= √3/3，b=2．所以直线AB的表达式为y= √3/3x+2

可得∠BAO=30°，∵∠BAC=60°，∴∠CAO=90°

在Rt△BAO中，由勾股定理得：AB=4．

∴AC=4，点C(-2√3，4)．

（2）∵点C、M都在第二象限，且△ABM的面积等于△ABC的面积，

∴CM∥AB．设直线CM的表达式为y=√3/3x+m，点C(-2√3，4)在直线CM上

∴m=6，∴直线CM的表达式为y=√3/3x+6

∴点M的坐标(-5√3,1)

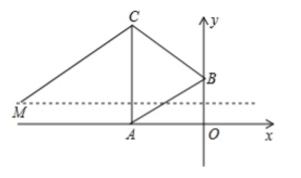
（3）由点C、M可得，CM：√((-2√3+5√3)²+3²)=6

①当⊙C与⊙N外切时，CN=CM+1=7；

在Rt△CAN中，AN=√(CM²-CA²)=√33

∴ON=AN+OA=√33+2√3或ON=AN-OA=√33-2√3

∴点N的坐标为：(-√33-2√3，0)、(√33-2√3，0)

②当⊙C与⊙N内切时，CN=CM-1=5；

在Rt△CAN中，CN=5，CA=4，则AN=3；

∴ON=AN+OA=3+2√3或ON=AN-OA=3-2√3

∴点N的坐标为：(-√3-2√3，0)、(3-2√3，0)

综上可知：点N的坐标为：(-√33-2√3，0)、(√33-2√3，0)、(-√3-2√3，0)、(3-2√3，0)

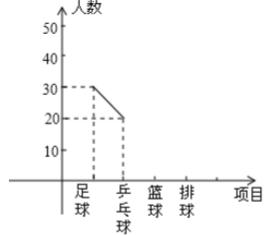
图2.1

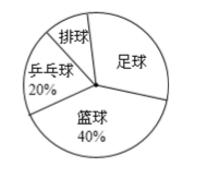
图2.2

2、学校为了响应国家阳光体育活动，选派部分学生参加足球、乒乓球、篮球、排球队集训．根据参加项目制成如下两幅不完整的统计图（如图2.1和如图2.2)，要求每位同学只能选择一种自己喜欢的球类，图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数）

请你根据图中提供的信息解答下列问题：

（1）参加篮球队的有____人，参加足球队的人数占全部参加人数的___ %．

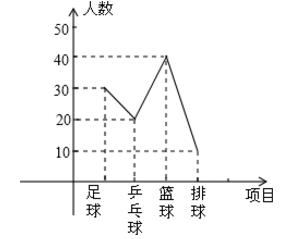
（2）喜欢排球队的人数在扇形统计图中所占的圆心角是多少度？并补全频数分布折线统计图．

（3）若足球队只剩一个集训名额，学生小明和小虎都想参加足球队，决定采用随机摸球的方式确定参加权，具体规则如下：一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球，小明随机地从四个小球中摸出一球然后放回，小虎再随机地摸出一球，若小明摸出的小球标有数字比小虎摸出的小球标有的数字大，则小明参加，否则小虎参加，试分析这种规则对双方是否公平？

解：（1）∵结合折线图与扇形图得出参加乒乓球队的人数为20，占总数的20%，

∴总人数为：20÷20%=100人， ∴参加篮球队的有：100×40%=40人，

参加足球队的人数占全部参加人数的：30÷100×100%=30%， 故答案为：40，30；

（2）喜欢排球队的人数在扇形统计图中所占的圆心角是百分比为：1-（40%+30%+20%）=10%，

圆心角度数=360×10%=36°；正确补全折线图中篮球、排球折线；

3、共有16种可能的结果，且每种结果的可能性相同，其中小明可能获得参加权的结果是六种

分别是2，1；3，1；3，2；4，1；4，2；4，3；

∴小明获参加权的概率P1=6/16=3/8，小虎获参加权的概率P2=10/16=5 /8，

∵P1＜P2， ∴这个规则对双方不公平．

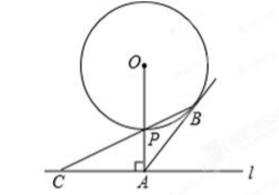
图3.1

3、如图3.1，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点 P，AB与⊙O相切于点B，BP的延长线交直线l于点C． 

（1）试判断线段AB与AC的数量关系，并说明理由；

（2）若PC=52，求⊙O的半径和线段PB的长；

（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．

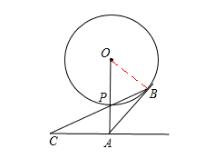
图3.2

解：

（1）AB=AC。理由如下： 连接OB。如图3.2

∵AB切⊙O于B，OA⊥AC，∴∠OBA=∠OAC=90°。

∴∠OBP+∠ABP=90°，∠ACP+∠CPB=90°。

∵OP=OB，∴∠OBP=∠OPB。

∵∠OPB=∠APC，∴∠ACP=∠ABC。 ∴AB=AC

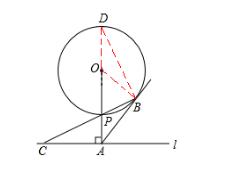
图3.3

（2）如图3.3延长AP交⊙O于D，连接BD，

设圆半径为r，则由OA=5得，OP=OB=r，PA=5－r。

又∵PC=2√5，

∴AB²=OA²-OB²=5²-r²，AC²=PC²-PA²=(2√5)²-(5-r)²

由（1）AB=AC得：(5-t)²=(2√5)²-(5-r)²，得：r=3。

∴AB=AC=4。 ∵PD是直径，∴∠PBD=90°=∠PAC。

∵∠DPB=∠CPA，∴△DPB∽△CPA

∴ CP/PD=AP/BP ，即2√5/6=2/BP，解得PB=6√5/5。

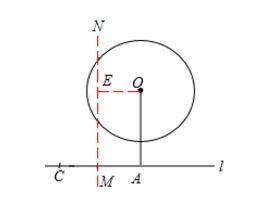
图3.4

（3）如图3.4，作线段AC的垂直平分线MN，作OE⊥MN，

则OE=1/2AC=1/2AB= 1/2√(5-r)²

又∵圆O要与直线MN交点，∴OE=1/2√(5-r)²≤r，

∴r≥√5。 又∵圆O与直线l相离，∴r＜5。

∴⊙O的半径r的取值范围为√5≤r＜5．