中考数学真题赏析「找规律——等比数列」

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

（2018年广东中考数学第16题）

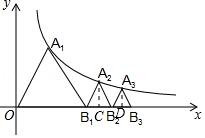
如图，已知等边△OA1B1，顶点A1在双曲线y=√3/x（x＞0）上，点B1的坐标为（2，0）．过B1作B1A2∥OA1交双曲线于点A2，过A2作A2B2∥A1B1交x轴于点B2，得到第二个等边△B1A2B2；过B2作B2A3∥B1A2交双曲线于点A3，过A3作A3B3∥A2B2交x轴于点B3，得到第三个等边△B2A3B3；以此类推，…，则点B6的坐标为 ．

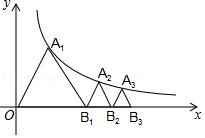
【答案】（2√6，0）．

【分析】解：如图，作A2C⊥x轴于点C，设B1C=a，则A2C=√3a，

OC=OB1+B1C=2+a，A2（2+a，√3a）．

∵点A2在双曲线y=√3/x（x＞0）上，

∴（2+a）•√3a=√3，

解得a=√2﹣1，或a=﹣√2﹣1（舍去），

∴OB2=OB1+2B1C=2+2√2﹣2=2√2，

∴点B2的坐标为（2√2，0）；

作A3D⊥x轴于点D，设B2D=b，则A3D=√3b，

OD=OB2+B2D=2√2+b，A2（2√2+b，√3b）．

∵点A3在双曲线y=√3/x（x＞0）上，

∴（2√2+b）•√3b=√3，

解得b=﹣√2+√3，或b=﹣√2﹣√3（舍去），

∴OB3=OB2+2B2D=2√2﹣2√2+2√3=2√3，

∴点B3的坐标为（2√3，0）；

同理可得点B4的坐标为（2√4，0）即（4，0）；

…，

∴点Bn的坐标为（2√n，0），

∴点B6的坐标为（2，0）．

（2018年贵港中考数学第18题）

如图，直线l为y=√3x，过点A1（1，0）作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画圆弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半径画圆弧交x轴于点A3；……，按此作法进行下去，则点An的坐标为（ ， ）．

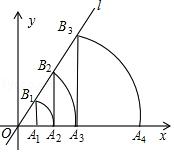
【答案】2n﹣1，0．

【分析】解：∵直线l为y=√3x，点A1（1，0），A1B1⊥x轴，

∴当x=1时，y=√3，

即B1（1，√3），

∴tan∠A1OB1=√3，

∴∠A1OB1=60°，∠A1B1O=30°，

∴OB1=2OA1=2，

∵以原点O为圆心，OB1长为半径画圆弧交x轴于点A2，

∴A2（2，0），

同理可得，A3（4，0），A4（8，0），…，

∴点An的坐标为（2n﹣1，0）．

（2018年安顺中考数学第18题）

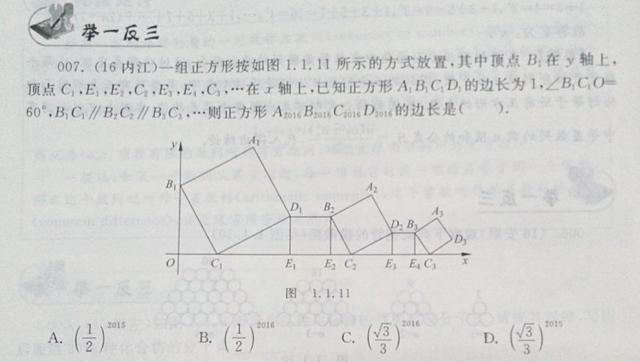
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置，点A1，A2，A3…和点C1，C2，C3…分别在直线y=x+1和x轴上，则点Bn的坐标为（ ， ）．

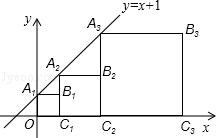
【答案】（2n﹣1，2n﹣1）．

【分析】解：当x=0时，y=x+1=1，

∴点A1的坐标为（0，1）．

∵四边形A1B1C1O为正方形，

∴点B1的坐标为（1，1）．

当x=1时，y=x+1=2，

∴点A2的坐标为（1，2）．

∵四边形A2B2C2C1为正方形，

∴点B2的坐标为（3，2）．

同理可得：点A3的坐标为（3，4），点B3的坐标为（7，4），点A4的坐标为（7，8），点B4的坐标为（15，8），…，

∴点Bn的坐标为（2n﹣1，2n﹣1）．

（2018年天门中考数学第16题）

如图，在平面直角坐标系中，△P1OA1，△P2A1A2，△P3A2A3，…都是等腰直角三角形，其直角顶点P1（3，3），P2，P3，…均在直线y=﹣1/3x+4上．设△P1OA1，△P2A1A2，△P3A2A3，…的面积分别为S1，S2，S3，…，依据图形所反映的规律，S2018=．

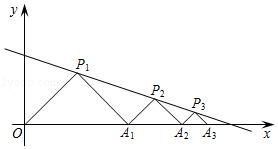
【答案】9/42017．

【分析】解：如图，分别过点P1、P2、P3作x轴的垂线段，垂足分别为点C、D、E，

∵P1（3，3），且△P1OA1是等腰直角三角形，

∴OC=CA1=P1C=3，

设A1D=a，则P2D=a，

∴OD=6+a，

∴点P2坐标为（6+a，a），

将点P2坐标代入y=﹣1/3x+4，得：﹣1/3（6+a）+4=a，

解得：a=3/2，

∴A1A2=2a=3，P2D=3/2，

同理求得P3E=3/4、A2A3=3/2，

∵S1=×6×3=9、S2=1/2×3×3/2=9/4、S3=1/2×3×3/4=9/16、……

∴S2018=9/42017．

（2018年衡阳中考数学第18题）

如图，在平面直角坐标系中，函数y=x和y=﹣1/2x的图象分别为直线l1，l2，过点A1（1，﹣1/2）作x轴的垂线交11于点A2，过点A2作y轴的垂线交l2于点A3，过点A3作x轴的垂线交l1于点A4，过点A4作y轴的垂线交l2于点A5，…依次进行下去，则点A2018的横坐标为 ．

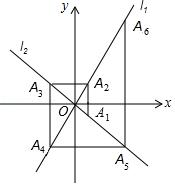
【答案】21008．

【分析】解：由题意可得，

A1（1，﹣1/2），A2（1，1），A3（﹣2，1），A4（﹣2，﹣2），A5（4，﹣2），…，

∵2018÷4=504…2，2018÷2=1009，

∴点A2018的横坐标为：21008．

（2018年淮安中考数学第16题）

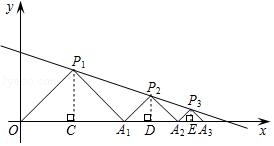
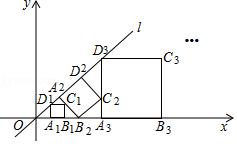
如图，在平面直角坐标系中，直线l为正比例函数y=x的图象，点A1的坐标为（1，0），过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x轴的垂线，垂足为A3，交直线l于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形AnBnCnDn的面积是 ．

【答案】（9/2）n﹣1．

【分析】解：∵直线l为正比例函数y=x的图象，

∴∠D1OA1=45°，

∴D1A1=OA1=1，

∴正方形A1B1C1D1的面积=1=（9/2）1﹣1，

由勾股定理得，OD1=√2，D1A2=√2/2，

∴A2B2=A2O=3√2/2，

∴正方形A2B2C2D2的面积=9/2=（9/2）2﹣1，

同理，A3D3=OA3=9/2，

∴正方形A3B3C3D3的面积=81/4=（9/2）3﹣1，

…

由规律可知，正方形AnBnCnDn的面积=（9/2）n﹣1．