例题1、古希腊数学家把数 1 , 3 , 6 , 10 ,15 , 21 ,...... 叫做三角形数,它有一定的规律性。若把第一个三角形数记为 a1 ,第二个三角形数记为 a2 ,......,第 n 个三角形数记为 an ,则 an + a(n+1) = ?
答案:(n + 1)^2 。
例题2、在平面直角坐标系中,对于平面内任意一点 P(a , b)若规定以下三种变换 :
① f(a , b)= (-a , b), 如 f(2 , 5)= (-2 , 5);
② g(a , b) = (b , a), 如 g(2 , 5)= (5 , 2);
③ h(a , b)= (-a , -b),如 h(2 , 5)= (-2 , -5) 。
根据以上变换,那么 f(h(5 , -3))等于多少 ?
答案:(5,3)。
例题3、如图,已知等腰直角 △ABC 的直角边长为 1 ,以 Rt△ABC 的斜边 AC 为直角边 ,画第二个等腰 Rt△ACD ,在以 Rt△ACD 的斜边 AD 为直角边 ,画第三个等腰 Rt△ADE , ... , 依次类推到第五个等腰 Rt△AFG ,则由这五个等腰直角三角形所构成的图形的面积是多少 ?
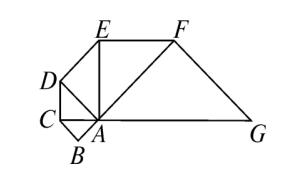
答案:31/2 。
例题4、如图所示,直线 OP 经过点 P(4,4√3),过 x 轴上的点 1、3、5、7、9、11 ......分别作 x 轴的垂线,与直线 OP 相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为 S1 , S2 , S3 , ... , Sn , 则 Sn 关于 n 的函数关系式是 ?
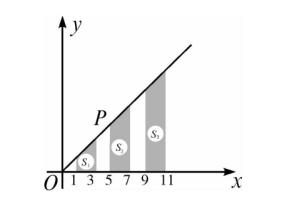
答案: Sn = 4√3 (2n - 1) 。
例题5、现将 1、 √2、√3、√6 四个数按下列方式排列 。
若规定 (m , n)表示第 m 排从左到右第 n 个数 , 则 (5 , 4)与(15 , 7)表示的两数之积是多少?

答案: 2√3 。
例题6、现将一块直角三角形的花圃进行改造,已知两直角边长分别为 6 m 、8 m 。若将其扩建成等腰三角形,且扩充部分是以 8 m 为直角边的直角三角形,那么扩建后的等腰三角形花圃的周长是多少 m ?
解:如图,在 Rt△ABC 中 ,∠ACB = 90° ,AC = 8 m, BC = 6 m,
由勾股定理得 : AB = 10 m ,扩充部分为 Rt△ACD 。
扩充成等腰△ABD ,应分以下三种情况:
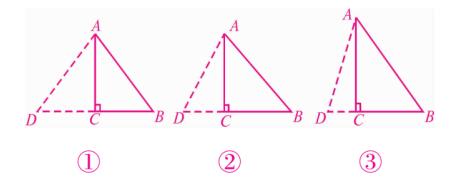
(1)如图 ① ,当 AB = AD = 10 m 时 ,可求得 CD = CB = 6 m ,
故 △ABD 的周长为 AB + AD + BD = 32 m ;
(2)如图 ② ,当 AB = BD = 10 m 时 ,可求得 CD = BD - BC = 4 ,
在 Rt△ACD 中 ,由勾股定理可得 AD = √(AC^2 + CD^2)= 4√5 ,
故 △ABD 的周长为 AB + BD + AD = (20 + 4√5) m ;
(3)如图 ③ ,当 AB 为底时 ,设 AD = BD = x ,则 CD = x - 6 ,
在 Rt△ACD 中 ,由勾股定理可得 AC^2 + CD^2 = AD^2 ,
所以 8^2 + (x - 6)^2 = x^2 , 解得: x = 25/3 ,
故 △ABD 的周长为 AB + BD + AD = 80/3 m 。
例题7、仔细观察下表后,请回答下列问题:
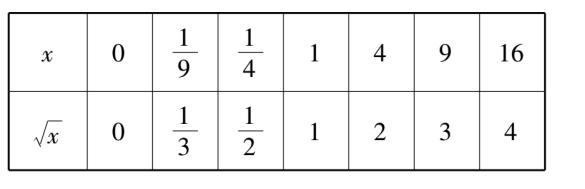
① 当正数 x 的值逐渐增大时,x 的算术平方根有什么变化规律?
② 正数 n 的算术平方根与它本身有怎样的大小关系 ?
③ 如果 10 的算术平方根为 a ,则 a 的整数部分是什么?小数部分又是什么?请说明理由。
解:
① x 的算术平方根也逐渐增大 ;
② 当 0 < n < 1 时 ,√n > n ;
当 n = 1 时 , √n = n ;
当 n > 1 时 , √n < n ;
③ a 的整数部分是 3 , 小数部分是 √10 - 3 。
理由:
∵ 9 < 10 < 16 , ∴ √9 = 3 < √10 = a < √16 = 4 ,
∴ a 的整数部分是 3 , 小数部分是 a - 3 (即 √10 - 3) 。
例题8、如图所示,BE 与 CD 相交于点 A ,CF 是 ∠BCD 的角平分线,EF 是 ∠BED 的角平分线,试求 ∠F 与 ∠B 、∠D 之间的数量关系,并说明理由 。
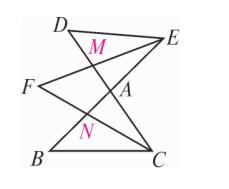
解:设 DC 、 EF 相交于点 M ,CF 、BE 相交于点 N ,
则有 : ∠DCF + ∠F = ∠D + ∠DEM ①,
∠F + ∠FEB = ∠B + ∠BCF ②,
① + ②, 得 (∠F +∠F )+ (∠DCF + ∠FEB)= (∠D + ∠B)+ (∠DEM + ∠BCF) ,
∵ CF 是 ∠BCD 的角平分线,EF 是 ∠BED 的角平分线,
∴ ∠DEM = ∠FEB , ∠BCF = ∠DCF ,
∴ ∠DCF + ∠FEB = ∠DEM + ∠BCF ,
∴ 2∠F = ∠D + ∠B 。
例题9、已知,用 2 辆 A 型车和 1 辆 B 型车装满货物一次可运货 10 吨 ;用 1 辆 A 型车和 2 辆 B 型车装满货物一次可运货 11 吨。某物流公司现有 31 吨货物,计划同时租用 A 型车 a 辆 , B 型车 b 辆 ,一次运完,且恰好每辆车都装满货物。根据以上信息,请回答下列问题 :
(1) 1 辆 A 型车和 1 辆 B 型车都装满货物一次可分别运货多少吨 ;
(2)请你帮该物流公司设计租车方案 ;
(3)若 A 型车每辆租金 100 元/次 ,B 型车每辆需租金 120 元/次 ,请选出最省钱的租车方案,并求出最少租车费 。
解:
(1)设 1 辆 A 型车和 1 辆 B 型车都装满货物一次可分别运货 x 吨 , y 吨 ,
根据题意得

故1 辆 A 型车和 1 辆 B 型车都装满货物一次可分别运货 3 吨 , 4 吨 。
(2)根据题意得,3a + 4b = 31 , 即 b = ( 31 - 3a ) / 4 ,
要使 a , b 都为正整数的情况共有三种情况 :
① a = 1 , b = 7 ;
② a = 5 , b = 4 ;
③ a = 9 , b = 1 。
故租车方案分别为 :
① A 型车 1 辆 , B 型车 7 辆 ;
② A 型车 5 辆 , B 型车 4 辆 ;
③ A 型车 9 辆 , B 型车 1 辆 。
(3)设车费为 w 元 ,则 w = 100a + 120b ,
方案 ① 花费为 100 × 1 + 120 × 7 = 940 元 ;
方案 ② 花费为 100 × 5 + 120 × 4 = 980 元 ;
方案 ③ 花费为 100 × 9 + 120 × 1 = 1020 元 。
故方案 ① 最省钱 ,即租用 A 型车 1 辆 ,B 型车 7 辆 时 ,最少租车费为 940 元 。
例题10、已知直线 AB 过点 A(2 , 1)和点 B ,其中点 B 是另一条直线 y = x + 2 与 y 轴的交点 。
(1)求直线 AB 的表达式 ;
(2)点 P 在直线 AB 上 ,是否存在点 P 使得 △BOP 的面积为 1 ,若存在,写出所有满足条件的点 P 的坐标,若不存在,请说明理由 。
(3)点 P 为直线 AB 上的一个动点 ,当点 P 在线段 AB 之间时,若 S△BOP = 2S△AOP ,求出此时点 P 的坐标 。
解:
(1)设直线 AB 的表达式为 y = kx + b ( k ≠ 0 ) ,
根据题意得 : A(2 ,1),B(0 ,2),
则有:1 = 2k + b , 2 = b ,
解得 :k = -1/2 ,
所以直线 AB 的表达式为 y = -1/2 x + 2 .
(2)设点 P 的坐标为 (a , -1/2 a + 2),
则 S△BOP = 1/2 OB ▪ ∣a∣= 1/2 × 2 ▪ ∣a∣ = ∣a∣ ,
∵ S△BOP = 1 , ∴ ∣a∣ = 1 , ∴ a = ±1 ,
∴ P 点的坐标为 (1 , 3/2)或 (-1,5/2)。
(3)设点 P 的坐标为 (a , -1/2 a + 2),
∵ S△BOP = 1/2 OB ▪ ∣a∣= 1/2 × 2 ▪ ∣a∣ = ∣a∣,
S△AOP = S△AOB - S△BOP = 2 - ∣a∣ ,
又 ∵ S△BOP =2 S△AOP ,
∴ ∣a∣ =2 ▪ ( 2 - ∣a∣) ,解得 :a = ±4/3 ,
∵ 点 P 在线段 AB 之间 , ∴ a = 4/3 ,
∴ P 点的坐标为 (4/3 ,4/3)。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论