小学、初中、高中各年级各学科学习资料,加微信:13353111130 领取!
一、实数的大小比较
有理数大小的比较法则在实数范围内仍然适用:
法则1:在数轴上表示的两个数,右边的点表示的数总比左边的点表示的数大;
法则2:正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小 。
二、比较两个实数的大小的常用方法:
(1)定义比较法;
例题1、比较
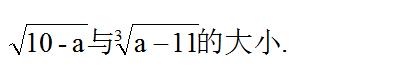
解:
∵ 10 - a ≥ 0 , ∴ a ≤ 10 , a - 11 < 0
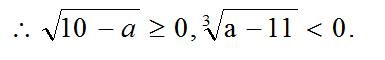
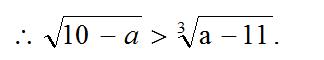
(2)作商比较法;
例题、比较
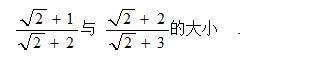
解:
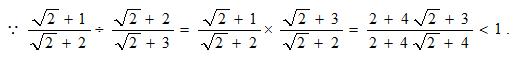
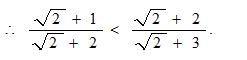
(3)取近似值比较法;
常用三个无理数的估算(精确到千分位)
√2 ≈ 1.414 , √3 ≈ 1.732 , √5 ≈ 2.236 。
例题、比较 √5 + 2 与 4.2 的大小 。
解:
∵ √5 ≈ 2.236 , ∴ √5 + 2 ≈ 4.236
又 ∵4.236 > 4.2
∴ √5 + 2 > 4.2
(4)平方比较法;
例题、比较 √6 + √10 与 √14 + √2 的大小 。
解:
∵ (√6 + √10)^2 = 16 + 4√15 , (√14 + √2)^2 = 16 + 4√7 ;
又∵ √15 > √7
∴ (√6 + √10)^2 > (√14 + √2)^2
∴ √6 + √10 > √14 + √2
(5)放缩比较法;
例题、比较 √6 + 2 与 √53 - 2 的大小 。
解:
∵ 2 < √6 < 3 , 7 < √53 < 8 ,
∴ √6 + 2 < 3 + 2 = 5 < √53 - 2
∴ √6 + 2 < √53 - 2
(6)倒数比较法;
例题、已知 a = √2019 - √2017 , b = √2018 - √2016 , 试比较 a , b 之间的大小 。
解:
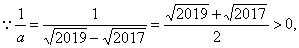
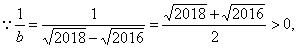
又∵ √2019 + √2017 > √2018 + √2016
∴ 1/a > 1/b
∴ a < b
(7)分子有理化比较法;
例题、比较 √17 - √14 与 √14 - √11 的大小 。
解:
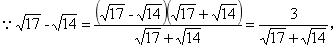
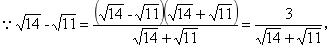
又∵ √17 + √14 > √14 + √11
∴ √17 - √14 < √14 - √11
(8)分母有理化比较法;
例题、比较
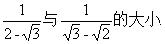
解:
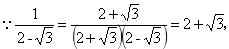
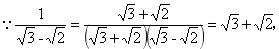
又 ∵ 2 + √3 > √3 + √2
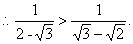

 加载中,请稍侯......
加载中,请稍侯......
精彩评论