八年级数学巧添辅助线

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

一、作平行线证明直线之间的位置关系

例题1、如图，已知 ∠B + ∠BCD + ∠D = 360° ，求证：AB∥DE 。

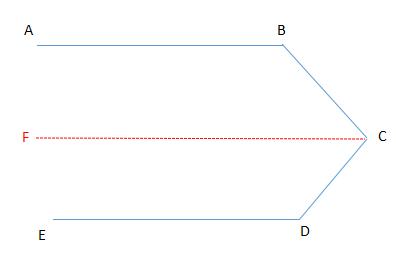
例题1图

证明：过点 C 作 CF∥AB

∵ CF∥AB ， ∴ ∠B + ∠BCF = 180° 。

又 ∵ ∠B + ∠BCD + ∠D = 360° ， ∴ ∠DCF + ∠D = 180° 。

∴ CF∥DE ，

∴ AB∥DE 。

二、作平行线探究角度之间的关系

例题2、如图，已知直线 L1 ∥ L2 ，直线 L3 和直线 L1、L2 交于点 C 和点 D ，在 C 、D 之间有一动点 P 。

① 若点 P 在 C 、 D 之间运动时，问 ∠PAC、∠APB、∠PBD 三者之间存在什么样的关系，请说明理由 ；

② 若点 P 在 C 、 D 两点的外侧运动时 （点 P 与点 C 、D 不重合），试探究 ∠PAC、∠APB、∠PBD 三者之间的关系 。

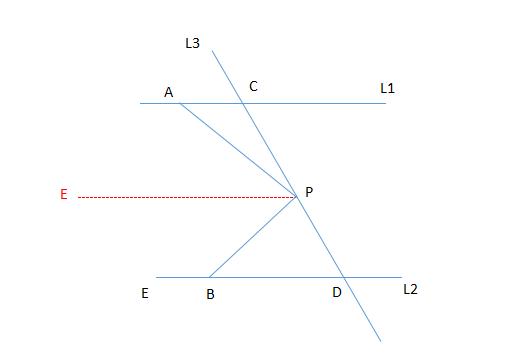
例题2图

解：

（1）若 点 P 在 C 、 D 之间运动时，则有 ∠APB = ∠PAC + ∠PBD 。

理由：过点 P 作 PE∥L1 ，则 ∠APE = ∠PAC ，

又 ∵ L1 ∥ L2 ，∴ PE∥L2 ，

∴ ∠BPE = ∠PBD ，

∴ ∠APE + ∠BPE = ∠PAC + ∠PBD ，

∴ ∠APB = ∠PAC + ∠PBD 。

（2） 若点 P 在 C 、 D 两点的外侧运动时 （点 P 与点 C 、D 不重合），则有两种情形：

① 如下图所示，

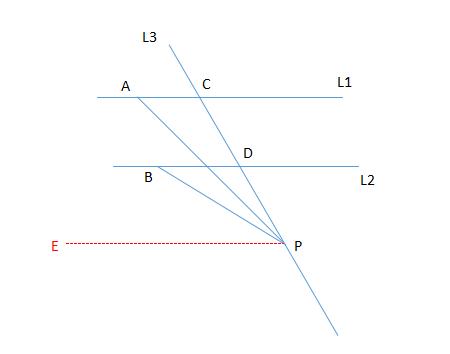
①图

结论：∠APB = ∠PAC - ∠PBD 。

理由：过点 P 作 PE∥L1 ，则 ∠APE = ∠PAC ，

又 ∵ L1∥L2 ，∴ PE∥L2 ，

∴ ∠BPE = ∠PBD ，

∵ ∠APE = ∠BPE + ∠APB ，

∴ ∠APB = ∠APE - ∠BPE ，

∴ ∠APB = ∠PAC - ∠PBD 。

② 如下图所示：

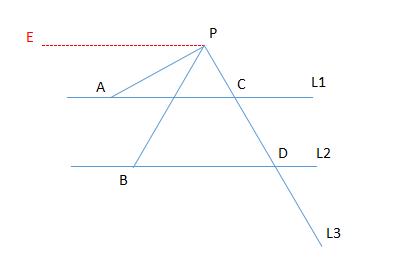
②图

结论：∠APB = ∠PBD - ∠PAC 。

理由：过点 P 作 PE∥L2 ，则 ∠BPE = ∠PBD 。

∵ L1∥L2 ， ∴ PE∥L1 ，

∴ ∠APE = ∠PAC ，

又∵ ∠APB = ∠BPE - ∠APE ，

∴ ∠APB = ∠PBD - ∠PAC 。

三、作平行线探究多边形角度之间的关系

例题3、如图，已知 AB ∥CD ，设 a = ∠A + ∠1 + ∠C，β = ∠B + ∠D ，则 a 与 β 之间有怎样的数量关系？试说明理由。

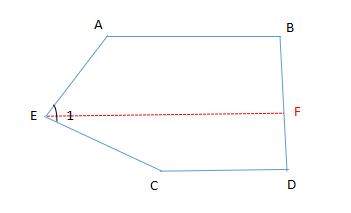
例题3图

解：a = 2β 。

理由：过点 E 作 EF∥AB ，交 BD 于点 F

∵ AB ∥CD ，∴ EF∥CD ，

∴ ∠A + ∠AEF = 180° ，∠C + ∠CEF = 180° ，∠B + ∠D = 180° ，

∴ a = ∠A + ∠AEF + ∠C + ∠CEF = 360° ， β = 180° ，

∴ a = 2β 。

四、作平行线解决实际问题

例题4、如图，一条公路修到湖边时，需要拐弯绕湖而过，如果第一次拐的 ∠A 是 120° ，第二次拐的 ∠B 是 150° ，第三次拐的是 ∠C ，这时的道路恰好和第一次拐弯前的道路平行，请问 ∠C 是多少度？请说明理由 。

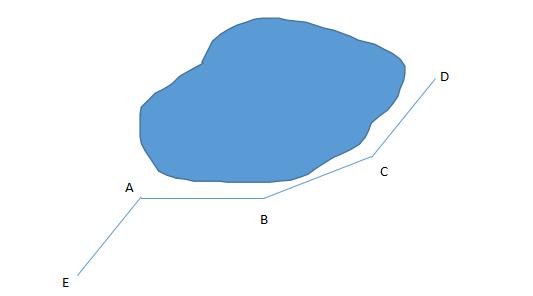
例题4图

解：如图，过点 B 作 BF∥AE ，

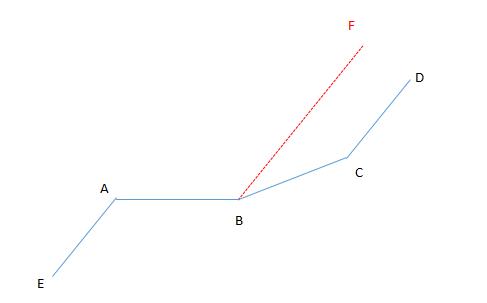
例题4答图

∴ ∠A = ∠ABF = 120° （两直线平行，内错角相等），

∴ ∠FBC = 30° ，

∵ AE∥CD ， ∴ BF∥CD ，

∴ ∠C = 180° - ∠FBC = 150° （两直线平行，同旁内角互补）