小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！
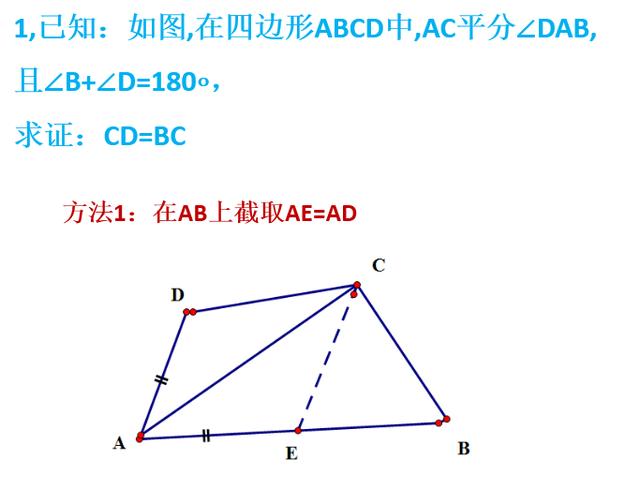
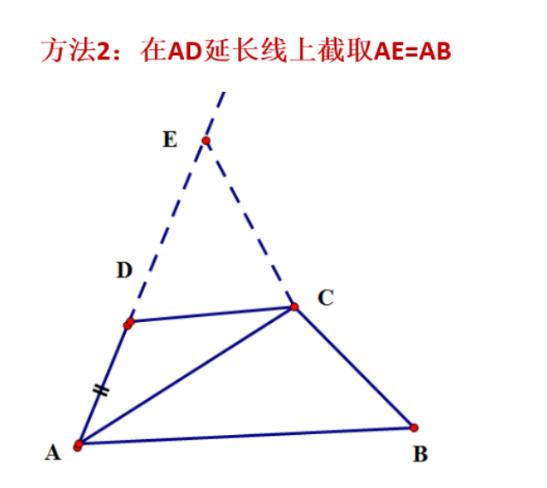
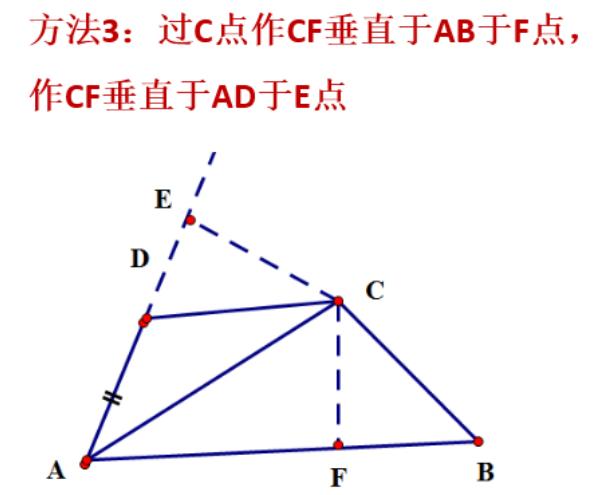
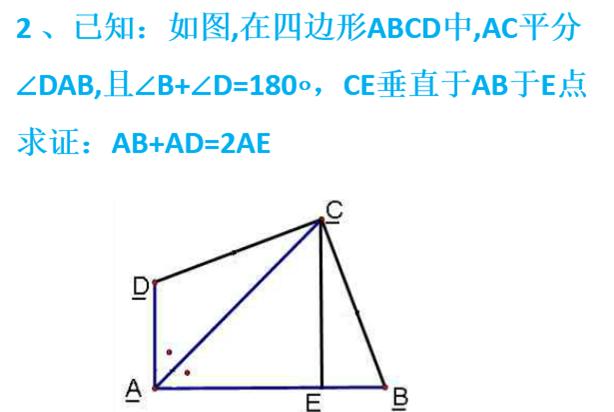
将图形放置到平面直角坐标系中，并且通过旋转变换，形成图形到证法都有所改变的变式，在结论中让同学体会二者的内在联系，形变而质不变的哲学原理
上一篇 : 初中数学因式分解最全资料，含例题 值得收藏
下一篇 : 初中数学暑假补习-动点问题7
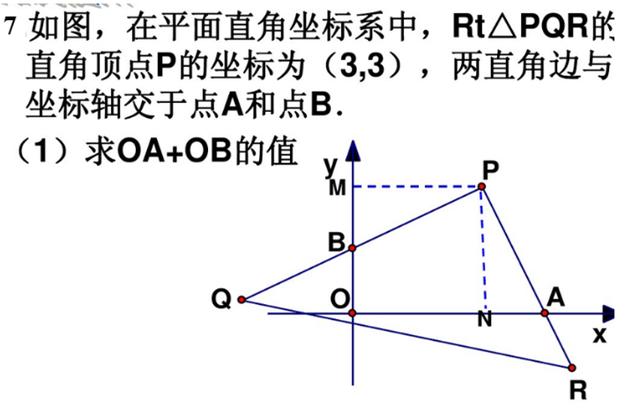
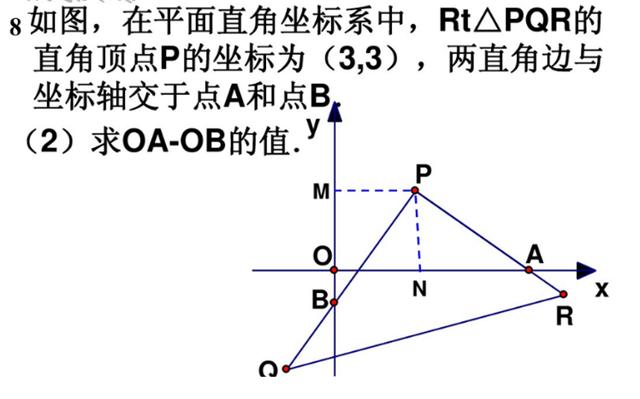
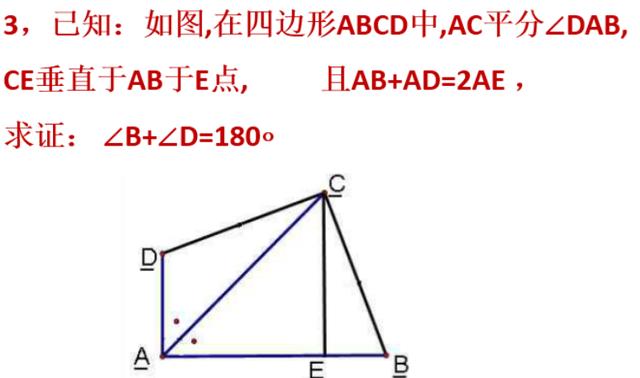
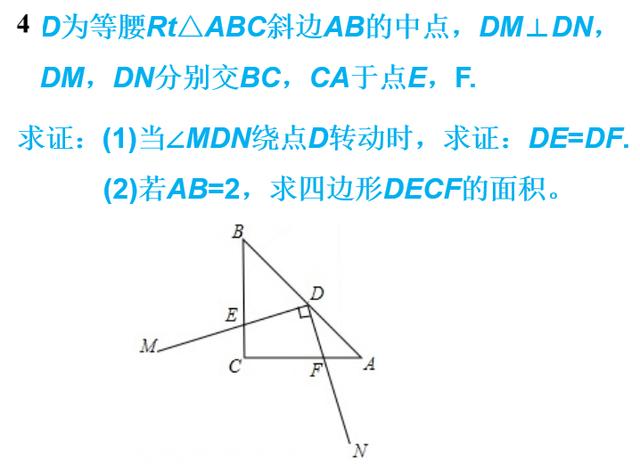
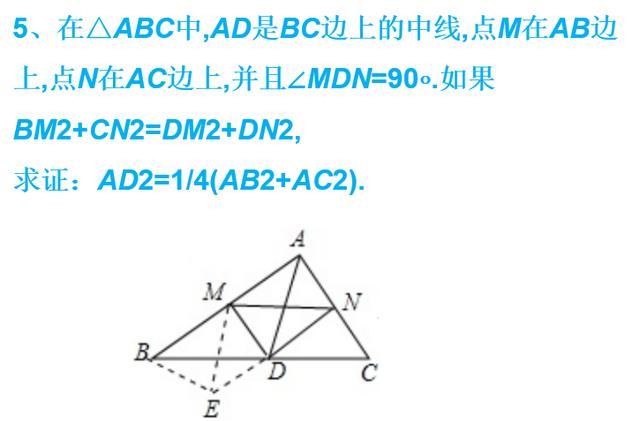
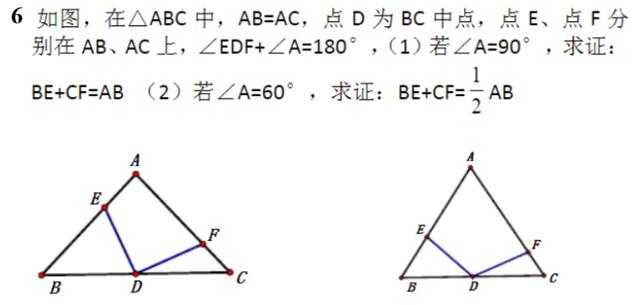
全等三角形中，一题多变与多题归一——对角互补模型
小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！
将图形放置到平面直角坐标系中，并且通过旋转变换，形成图形到证法都有所改变的变式，在结论中让同学体会二者的内在联系，形变而质不变的哲学原理
上一篇 : 初中数学因式分解最全资料，含例题 值得收藏
下一篇 : 初中数学暑假补习-动点问题7
初中数学，“将军饮马”的七大模型
人教版八年级数学上册第一章单元测试题（含答案）
初二《全等三角形》数学模型之“一线三等角”模型
加载中,请稍侯......
精彩评论