初中数学：梯形的五种常用辅助线添加方法

小学、初中、高中各年级各学科学习资料，加微信：13353111130 领取！

口诀：梯形问题如何巧转换，平移腰，平移对角线，做一高或两高，两腰延长三角形。如果出现有中点，细心连上中位线。上述方法不凑效，过腰中点全等造。

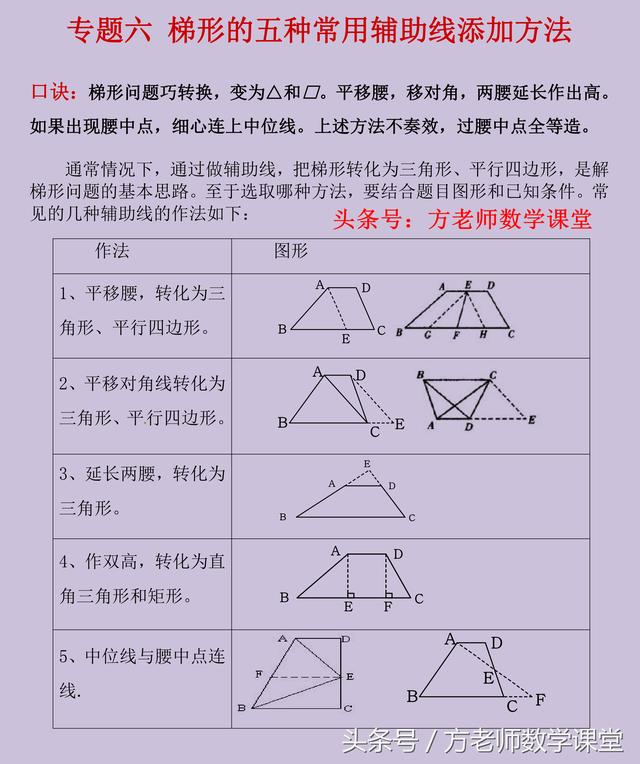
通常情况下，和梯形有关的几何题，辅助线的添加方法，有如上表格里的五种：

①平移腰，转化为三角形或者平行四边形；②平移对角线转化为三角形或者平行四边形；③延长两腰，转为三角形；④做高或者双高，转化为直角三角形或者矩形；⑤中位线与腰中点的连线。

在这五大类中，还有细分的一些小类。请大家细心的看下面的例题，一共举例了17道例题，经典考试题型，有详细解题步骤。后面，还有8道练习题。过瘾吧？那就疯狂点赞吧。

例1、有一个角是90°，通常根据题意，平移一腰，则出现直角三角形，用解直角三角形的思路，即可。

例2、平移一腰，得到一个三角形，通过三角形的三边关系定理。两边之和大于第三边，两边之差小于第三边，即可得出第三边的取值范围。

例3、平移两腰的经典考试题型。平移两腰，在梯形的中间得出一个三角形。

例4、平移对角线，得出一个平行四边形，再转化成一个三角形来解决问题。

例5，也是平移对角线，得到一个平行四边形和三角形，通过线段的转化，符合勾股定理，得出角度等于90°。

例6，平移对角线，得出平行四边形，还有等底等高三角形面积相等。此题非常巧妙。

例7，延长两腰，相交得出一个三角形。再利用原梯形的上底下底平行的关系，得出结论。

例8、这是一道证明四边形是等腰梯形的经典考试题型，不可错过的好题。请看详细解题推理步骤。

例9，连接对角线，也是解决梯形问题里一个辅助线添加方法。这题简单，但是这个BD的连接，是解题的关键。

例10，做梯形的一条高。证明四边形是等腰梯形。请看详细解题步骤，学会类似方法，举一反三。

例11、梯形做双高，得到一个矩形，和两个直角三角形，问题迎刃而解。

例12、这道题很新颖，求证两线段的大小关系。做双高，得到两个直角三角形和一个矩形，通过线段大小关系，结合勾股定理，顺利得证。证明线段大小关系的题，同学也要学会这类方法，举一反三。

例13、做中位线，已知梯形一腰的中点，做梯形的中位线。梯形的中位线等于上底加下底之和的一半。

例14、已知梯形的两条对角线的中点，连接梯形一顶点与一条对角线的中点，延长并与底边相交，转为三角形中位线，得出结论。

例15、梯形中出现一腰上的中点时，过这一点，构造出两个三角形全等。

例16、在梯形中，已知一腰的中点，证明两线段时间的大小关系。依然是通过这个腰上的中点构造出两个三角形全等。

例17、过腰的中点做另一条腰的平行线，与两底分别相交，得到两个三角形全等和一个平行四边形。

这8道练习题，考试真题精选，不是很难，都是非常基础的题。