小学、初中、高中各年级各学科学习资料,加微信:13353111130 领取!
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、
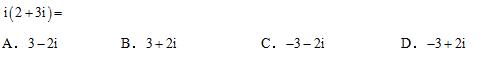
第1题图
2、
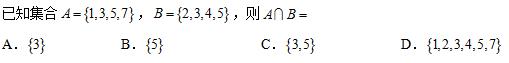
第2题图
3、
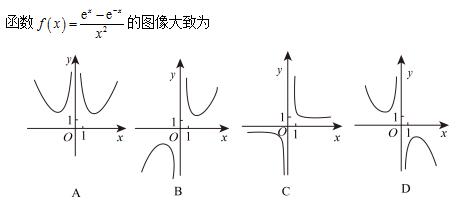
第3题图
4、
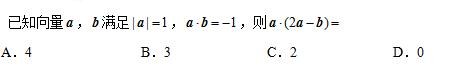
第4题图
5、从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为
A. 0.6 B.0.5 C.0.4 D.0.3
6、

第6题图
7、
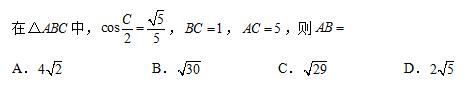
第7题图
8、
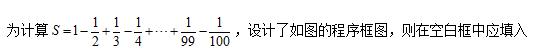
第8题图(1)
第8题图(2)
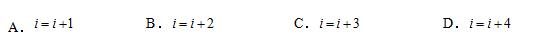
第8题图(3)
9、

第9题图
10、

第10题图
11、

第11题图
12、

第12题图
二、填空题:本题共4小题,每小题5分,共20分。
13、曲线 y = lnx 在点 (1 , 0)处的切线方程为__________。
14、若 x , y 满足约束条件
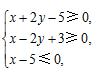
第14题图
则 z = x + y 的最大值为__________。
15、已知
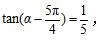
第15题图
则 tan a = __________。
16、已知圆锥的顶点为 S,母线 SA ,SB 互相垂直,SA 与圆锥底面所成角为 30° ,若 △SAB 的面积为 8,则该圆锥的体积为__________。
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23为选考题。考生根据要求作答。
(一)必考题:共60分。
17、(12分)
记 Sn 为等差数列 {an} 的前 n 项和,已知 a1 = -7 ,S3 = -15 .
(1)求 {an} 的通项公式;
(2)求 Sn ,并求 Sn 的最小值 。
18、(12分)下图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图。
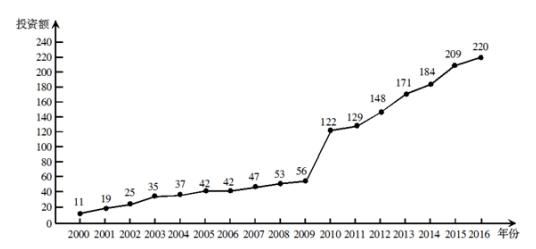
第18题图(1)
为了预测该地区2018年的环境基础设施投资额,建立了 y 与时间变量 t 的两个线性回归模型。
根据2000年至2016年的数据(时间变量 t 的值依次为 1,2,...,17)建立模型①:
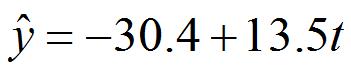
第18题图(2)
根据2010年至2016年的数据(时间变量 t 的值依次为 1,2,...,7)建立模型②:
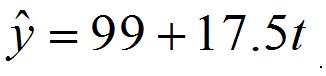
第18题图(3)
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由。
19、(12分)如图,在三棱锥 P-ABC 中,AB = BC = 2√2 ,PA = PB = PC = AC = 4 ,O 为 AC 的中点。
(1)证明:PO⊥平面ABC;
(2)若点 M 在棱 BC 上,且 MC = 2MB ,求点 C 到平面 POM 的距离。
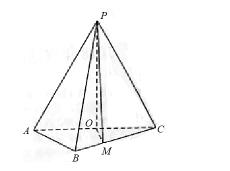
第19题图
20、(12分)

第20题图
21、(12分)
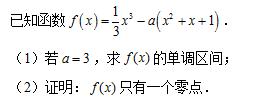
第21题图
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22、[选修4-4:坐标系与参数方程](10分)

第22题图
23、[选修4-5:不等式选讲](10分)

第23题图
2018年普通高等学校招生全国统一考试
文科数学试题参考答案

参考答案图(1)

参考答案图(2)

参考答案图(3)

参考答案图(4)

参考答案图(5)
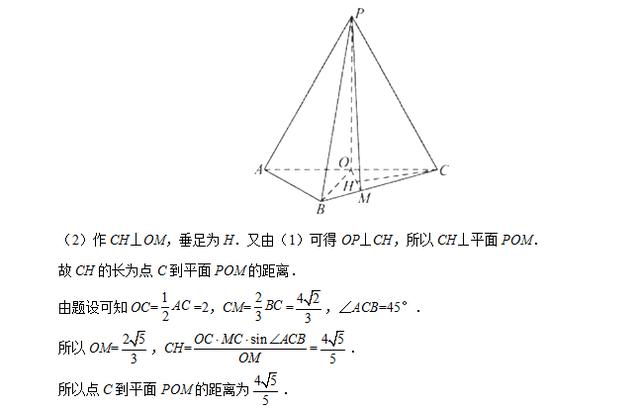
参考答案图(6)

参考答案图(7)

参考答案图(8)

参考答案图(9)
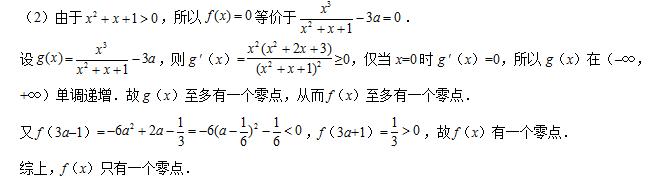
参考答案图(10)

参考答案图(11)

参考答案图(12)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论