1.等式:用“=”号连接而成的式子叫等式.
2.等式的性质:
等式性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;
等式性质2:等式两边都乘以(或除以)同一个不为零的数,所得结果仍是等式.
3.方程:含未知数的等式,叫方程.
4.方程的解:使等式左右两边相等的未知数的值叫方程的解;注意:“方程的解就能代入”!
5.移项:改变符号后,把方程的项从一边移到另一边叫移项.移项的依据是等式性质1.
6.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程.
7.一元一次方程的标准形式: ax+b=0(x是未知数,a、b是已知数,且a≠0).
8.一元一次方程解法的一般步骤:
化简方程----------分数基本性质
去 分母----------同乘(不漏乘)最简公分母
去 括号----------注意符号变化
移 项----------变号
合并同类项--------合并后注意符号
系数化为1---------未知数细数是几就除以几
知能点1:市场经济、打折销售问题
(1)商品利润=商品售价-商品成本价 (2)商品利润率=

×100%
(3)商品销售额=商品销售价×商品销售量(4)商品的销售利润=(销售价-成本价)×销售量
(5)商品打几折出售,就是按原价的百分之几十出售,如商品打8折出售,即按原价的80%出售.
1. 某商店开张,为了吸引顾客,所有商品一律按八折优惠出售,已知某种皮鞋进价60元一双,八折出售后商家获利润率为40%,问这种皮鞋标价是多少元?优惠价是多少元?
解:设这种皮鞋标价是x元
8/10x=60×(1+40%)
解得:x=105
105×8/10=84(元)
答:这种皮鞋标价是105元,优惠价是84元
3.一家商店将一种自行车按进价提高45%后标价,又以八折优惠卖出,结果每辆仍获利50元,这种自行车每辆的进价是多少元?若设这种自行车每辆的进价是x元,那么所列方程为( B )
A.45%×(1+80%)x-x=50 B. 80%×(1+45%)x - x = 50
C. x-80%×(1+45%)x = 50 D.80%×(1-45%)x - x = 50
解析: 因为 自行车按进价提高45%后标价, 已经设过自行车进价是X元了 所以 X(1+45%)=145%X ——也就是标价 因为 (标价)又以八折优惠卖出 所以 标价×八折=销售价 145%X × 0.8 = 1.16 X 因为 结果每辆获利50元 (获益 = 销售价 - 进价 ) 所以 获利的50元 = 销售价1.16X元 - 进价X元 上为解题思路, 得到方程 : 145%X • 0.8 - X =50
4.某商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多打几折.
解析:按最少利润为800*5%=40,则出售价为800+40=840,则打折为840/1200=70%,最低可以打七折
5.一家商店将某种型号的彩电先按原售价提高40%,然后在广告中写上“大酬宾,八折优惠”.经顾客投拆后,拆法部门按已得非法收入的10倍处以每台2700元的罚款,求每台彩电的原售价.
解:设每台彩电零售价为x.
[(1+40%)×80%]x-x=2700÷10
x=2250
答:每台彩电零售价为2250元.
知能点2: 方案选择问题
6.某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是: 如果对蔬菜进行精加工,每天可加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季度等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行粗加工,没来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为哪种方案获利最多?为什么?
方案三获利多
方案一:140*4500=630000
方案二:15*6=90 90*7500=675000 (140-90)*1000=50000 675000+50000=725000
方案三:设粗加工x天 16*x+6*(15-x)=140 x=5天
精加工15-5=10天
5*16*4500+10*6*7500=360000+450000=810000
7.某市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元月基础费,然后每通话1分钟,再付电话费0.2元;“神州行”不缴月基础费,每通话1分钟需付话费0.4元(这里均指市内电话).若一个月内通话x分钟,两种通话方式的费用分别为y1元和y2元.
(1)写出y1,y2与x之间的函数关系式(即等式).
(2)一个月内通话多少分钟,两种通话方式的费用相同?
(3)若某人预计一个月内使用话费120元,则应选择哪一种通话方式较合算?
(1)全球通:50+0.2*X
神州行:0.4X
(2) 50+0.2X=0.4X 得X=250
(3)50+0.2*120=74
0.4*120=48
选择神州行更优惠!
8.某地区居民生活用电基本价格为每千瓦时0.40元,若每月用电量超过a千瓦时,则超过部分按基本电价的70%收费。(1)某户八月份用电84千瓦时,共交电费30.72元,求a.
(2)若该用户九月份的平均电费为0.36元,则九月份共用电多少千瓦时?应交电费是多少元?
(1)0.5a+(80-a)×0.3=30 (2)设九月份用电度数为Y,则:
0.5a+24-0.3a=30 <30×0.5+(Y-30)×0.5>÷X=0.36
0.5a-0.3a=30-24 ( 15+0.3Y-9)÷X=0.36
0.2a=6 6+0.3Y=0.36Y
a=30 0.06Y=6
Y=100
知能点3储蓄、储蓄利息问题
(1)顾客存入银行的钱叫做本金,银行付给顾客的酬金叫利息,本金和利息合称本息和,存入银行的时间叫做期数,利息与本金的比叫做利率。利息的20%付利息税
(2)利息=本金×利率×期数 本息和=本金+利息 利息税=利息×税率(20%)
(3)

11. 某同学把250元钱存入银行,整存整取,存期为半年。半年后共得本息和252.7元,求银行半年期的年利率是多少?(不计利息税)
设半年期的利率是X可得方程式:
250*(1+1/2X)=252.7
解出X=2.16%
因为银行挂牌的利率全部都是年化的利率,半年期不足1年,因此,只有1/2!
一年2.25
三年2.70
六年2.88
12. 为了准备6年后小明上大学的学费20000元,他的父亲现在就参加了教育储蓄,下面有三种教育储蓄方式:
(1)直接存入一个6年期;
(2)先存入一个三年期,3年后将本息和自动转存一个三年期;
(3)先存入一个一年期的,后将本息和自动转存下一个一年期;你认为哪种教育储蓄方式开始存入的本金比较少?
1.解设存六年期的本金x元 列方程x(1+6×2.88%)=20000解得x=17053
2.设存入两个三年期的开始本金为y元 列方程y(1+2.7%×3)×(1+2.7%×3)=20000解得x=17115
3设存一年期本金为z元 列方程(1+2.25%)z=20000解得x=17894
13.小刚的爸爸前年买了某公司的二年期债券4500元,今年到期,扣除利息税后,共得本利和约4700元,问这种债券的年利率是多少(精确到0.01%).
设年利率是X
4500×2×X×(1-5%)=4700-4500
9000×95%X=200
8550X=200
X=200÷8550
X≈2.34%
知能点4:工程问题
工作量=工作效率×工作时间 工作效率=工作量÷工作时间
工作时间=工作量÷工作效率 完成某项任务的各工作量的和=总工作量=1
17. 一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
设乙还要x天完成。
因为甲独做15天完成,乙独做12天完成,所以甲的工作效率是1/15,乙的工作效率是1/12,列得:
3*(1/15+1/12)+x*(1/12)=1
x*(1/12)=11/20
x=33/5=6又5/3 约7天
答:乙还要33/5天才能完成全部工程。
18. 一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单独开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?
甲注水工效1/6
乙注水工效1/8
丙排水工效1/9
甲乙同时开放2小时,注水:
1/6×2+1/8×2=7/12
同时打开甲乙丙,每小时注水:
1/6+1/8-1/9=13/72
注满还需要:
(1-7/12)÷13/72=30/13小时
注满还需要x小时
(1/6+1/8-1/9)x=1-(1/6+1/8)*2
13/72x=5/12
x=30/13
19.一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?
总工程量为1 甲的速度是x 乙的是y
6x=1 x=1/6 4y=1 y=1/4 30/60 *1/6 +(1/4+1/6)z=1 z=2.2 小时
知能点5:若干应用问题等量关系的规律
(1)和、差、倍、分问题 此类题既可有示运算关系,又可表示相等关系,要结合题意特别注意题目中的关键词语的含义,如相等、和差、几倍、几分之几、多、少、快、慢等,它们能指导我们正确地列出代数式或方程式。 增长量=原有量×增长率 现在量=原有量+增长量
(2)等积变形问题
常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.
①圆柱体的体积公式 V=底面积×高=S·h=
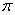
r2h
②长方体的体积 V=长×宽×高=abc
22.某粮库装粮食,第一个仓库是第二个仓库存粮的3倍,如果从第一个仓库中取出20吨放入第二个仓库中,第二个仓库中的粮食是第一个中的
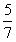
。问每个仓库各有多少粮食?
设第一仓原有3x吨,第二仓原有x吨
(3x-20)*5/7=x+20
5(3x-20)=7(x+20)
15x-100=7x+140
8x=240
x=30
3x=3×30=90
答:第一仓原有90吨,第二仓原有30吨
24.长方体甲的长、宽、高分别为260mm,150mm,325mm,长方体乙的底面积为130×130mm2,又知甲的体积是乙的体积的2.5倍,求乙的高?
设乙的高为hmm,根据题意得:
260×150×325=130×130×h×2.5,
解得:h=300(mm).
答:乙的高为300mm.
知能点6:行程问题
基本量之间的关系: 路程=速度×时间 时间=路程÷速度 速度=路程÷时间
(1)相遇问题 (2)追及问题
快行距+慢行距=原距 快行距-慢行距=原距
(3)航行问题 顺水(风)速度=静水(风)速度+水流(风)速度
逆水(风)速度=静水(风)速度-水流(风)速度
抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.
26. 甲乙两人在同一道路上从相距5千米的A、B两地同向而行,甲的速度为5千米/小时,乙的速度为3千米/小时,甲带着一只狗,当甲追乙时,狗先追上乙,再返回遇上甲,再返回追上乙,依次反复,直至甲追上乙为止,已知狗的速度为15千米/小时,求此过程中,狗跑的总路程是多少?
设两人相遇需要时间x小时,则由题意可列方程,
3x+5=5x,
5x-3x=5,
x=5÷2,
x=2.5;
由于小狗一只在二人之间来回一直跑,没有停,所以到甲追上乙时,小狗总共跑了:15×2.5=37.5(千米),
答:狗跑的总路程是37.5千米.
27. 某船从A地顺流而下到达B地,然后逆流返回,到达A、B两地之间的C地,一共航行了7小时,已知此船在静水中的速度为8千米/时,水流速度为2千米/时。A、C两地之间的路程为10千米,求A、B两地之间的路程。
C,B两地之间的路程是x千米
(10+x)/(8+2)+x/(8-2)=7
x=22.5
22.5+10=32.5
A,B两地之间的路程是32.5千米
28.有一火车以每分钟600米的速度要过完第一、第二两座铁桥,过第二铁桥比过第一铁桥需多5秒,又知第二铁桥的长度比第一铁桥长度的2倍短50米,试求各铁桥的长.
设第一桥长a,第二桥长b
600米/分=10米/秒
b-a=10*5=50m
b=a+50
b=2a-50
2a-50=a+50
a=100
b=150
知能点7:数字问题
(1)要搞清楚数的表示方法:一个三位数的百位数字为a,十位数字是b,个位数字为c(其中a、b、c均为整数,且1≤a≤9, 0≤b≤9, 0≤c≤9)则这个三位数表示为:100a+10b+c。然后抓住数字间或新数、原数之间的关系找等量关系列方程.
(2)数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
33. 一个三位数,三个数位上的数字之和是17,百位上的数比十位上的数大7,个位上的数是十位上的数的3倍,求这个三位数.
设十位上的数字为x,则个位上的数字为3x,百位上的数字是(x+7),
由题意得:3x+x+(x+7)=17,
解得:x=2,
即可得个位数字为6,十位数字为2,百位数字为9,
答:这个三位数为926.
34. 一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得的两位数比原两位数大36,求原来的两位数
设原十位数为X,个位数为2X,原两位数为(10X+2X).
(2X*10+X)-(10X+2X)=36
(20X+X)-(10X+2X)=36
21X-12X=36
9X=36
X=4
原两位数=10X+2X=10×4+2×4=48
答:原来的两位数是48.
注意:虽然我们分了几种类型对应用题进行了研究,但实际生活中的问题是千变万化的,远不止这几类问题。因此我们要想学好列方程解应用题,就要学会观察事物,关心日常生产生活中的各种问题,如市场经济问题等等,要会具体情况具体分析,灵活运用所学知识,认真审题,适当设元,寻找等量关系,从而列出方程,解出方程,使问题得解!
 加载中,请稍侯......
加载中,请稍侯......
精彩评论