抓特征，巧选择，妙解一元二次方程

一、 直接开平方法 --两个式子的平方相等，两者关系必然相等或相反

注意：正数或0 都能写成平方形式，而负数不可以，这就是上面强调P值为非负数的原因所在。

看一下用直接开平方法是不是非常简单（注意第2题括号前的4 、25分别看成2 、5的平方，把底数乘到括号里）

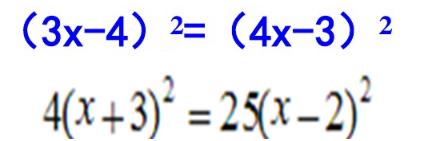
二、 配方法

比较一下两个方程，在配方过程中的区别

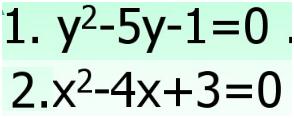
b=-5，加的是分数5/2的平方；b=-4，加的是整数2的平方.显然，第一个因为分数的出现，计算中会增加了难度，那么我们一般不选择配方法，而选择公式法

三公式法

四、 因式分解法：适合的题目，就归结为两种类型（仅从简单这一角度说的）

1、十字相乘法，建议只有各个系数都是较小的整数时采纳，毕竟此法不是万能方法，属于巧妙拼凑，当数较大时，即便能够解的出来，也费时费力，反而不如使用配方或者公式法更简单一些。

2、系数c=0类型

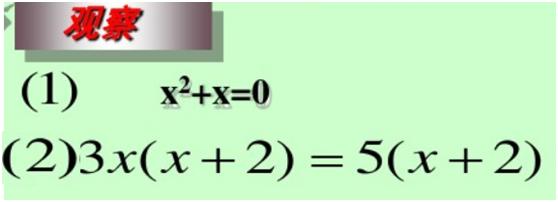
第1题c=0，两个解分别是0 、-1

第2题把（x+2）看成未知数y，左右Y的系数分别是3x、 5。

化为两个方程（x+2）=0 或3x=5

特别强调：仔细观察得到这两个方程的方法，中间完全可以省却移项、提公因式、方程再移项的过程，今后可以直接写出哦，那是相当的简单！！！

总结：通过以上分析，我们作出一下判断。

看到方程，观察特征，按照最简化原则，选择的顺序：直接开平方----因式分解------配方或公式法

练习：