例1、设数列 { an } 的前 n 项和为 Sn .已知 a1 = 1 ,
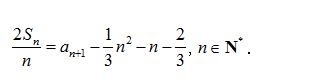
例题1图(1)
(1)求 a2 的值 ;
(2)求数列 { an } 的通项公式;
(3)证明: 对一切正整数 n ,有
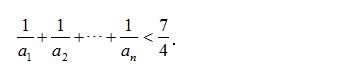
例题1图(2)
解:
(1)依题意, 2S1 = a2 - 1/3 - 1 - 2/3 , 又 S1 = a1 = 1 , 所以 a2 = 4 ;
(2)当 n ≥ 2 时,有
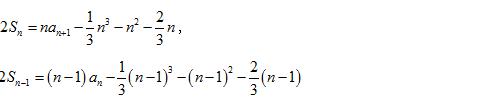
例题1图(3)
两式相减得
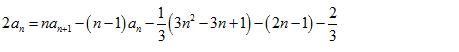
例题1图(4)
整理得
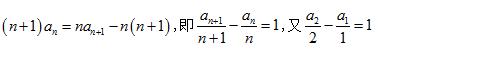
例题1图(5)
故数列 { an/n } 是首项为 a1/1 ,公差为 1 的等差数列,
所以
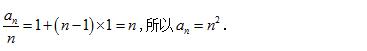
例题1图(6)
(3)当 n = 1 时 ,1/a1 = 1 < 7/4 ; 当 n = 2 时 ,1/a1 + 1/a2 = 1 + 1/4 = 5/4 < 7/4 ;
当 n = 3 时
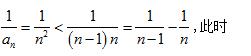
例题1图(7)
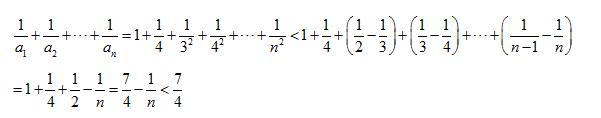
例题1图(8)
综上,对一切正整数 n ,有

例题1图(9)
放缩技巧:
所谓放缩的技巧:即欲证 A ≤ B ,欲寻找一个(或多个)中间变量 C ,使 A ≤ C ≤ B ,
由 A 到 C 叫做 “放”,由 B 到 A 叫做 “缩” 。
常用的放缩技巧
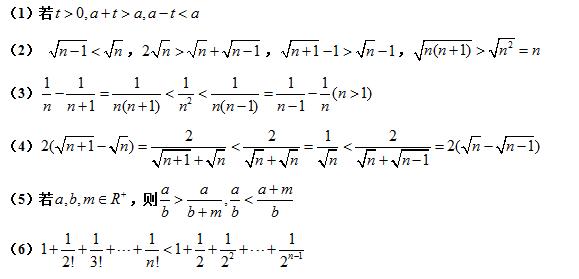
常用的放缩技巧图(1)
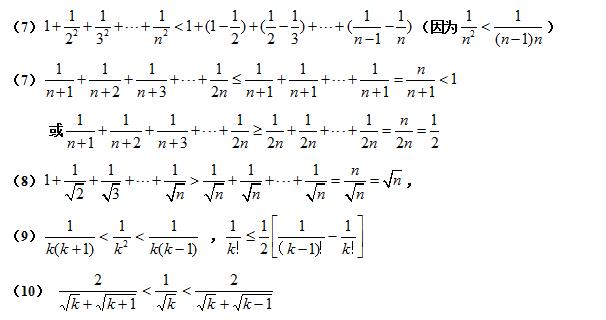
常用的放缩技巧图(2)
放缩方法归纳:
① 先求和后放缩
例题2、正数数列 {an} 的前 n 项的和为 Sn ,且满足关系式 2✔Sn = an + 1 ,试求:
(1)数列 {an} 的通项公式;
(2)设 bn = 1/(an·an+1), 数列 { bn } 的前 n 项和为 Bn , 求证 : Bn < 1/2 。
解:
(1)由已知得 4Sn = ( an + 1)^2 , n ≥ 2 时,
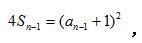
例题2图(1)
作差得:
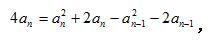
例题2图(2)
所以:
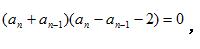
例题2图(3)
又因为 {an} 是正数数列,所以 an - an-1 = 2 , 即 {an} 是以公差为 2 的等差数列 ,
由 2✔S1 = a1 + 1 , 得 a1 = 1 , 所以 an = 2n - 1 。
(2)
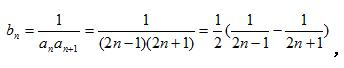
例题2图(4)
所以:
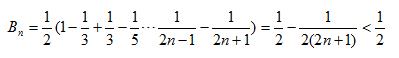
例题2图(5)
注:一般先分析数列的通项公式。
如果此数列的前 n 项和能直接求和或者通过变形后求和,则采用先求和再放缩的方法来证明不等式。
② 先放缩再求和
例题3、已知各项均为正数的数列 {an} 的前 n 项和为 Sn , 且满足关系式 (an)^2 + an = 2Sn 。
(1)求证:
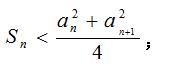
例题3图(1)
(2)求证:
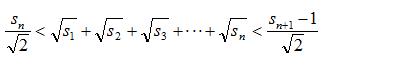
例题3图(2)
解:
(1)令 n = 1 , 则有 (a1)^2 + a1 = 2S1 = 2a1 , 因为 a1 > 0 , 所以 a1 = 1 。
又因为 (an)^2 + an = 2Sn ,有
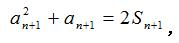
例题3图(3)
上述两式相减,且 an+1 = Sn+1 - Sn 得
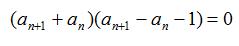
例题3图(4)
因为 an > 0 , 所以 an+1 - an = 1 所以 an = 1 + 1 × (n - 1)= n , Sn = n(n+1)/2 。
所以
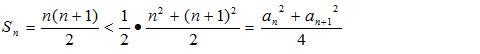
例题3图(5)
(2)
因为
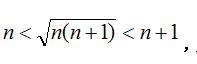
例题3图(6)
所以
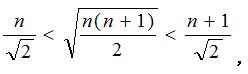
例题3图(7)
所以
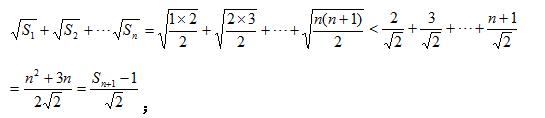
例题3图(8)
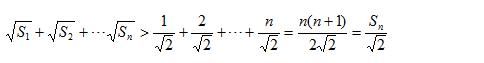
例题3图(9)
③ 裂项放缩
例题4、已知 n 是正整数,求证:
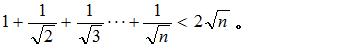
例题4图(1)
证明:
因为
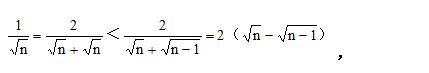
例题4图(2)
所以
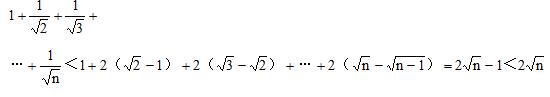
例题4图(3)
④ 公式放缩
例题5、已知函数
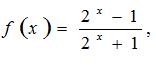
例题5图(1)
.证明:

例题5图(2)
证明:
因为
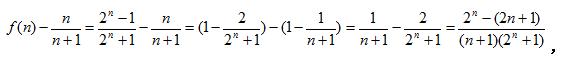
例题5图(3)
又因为 n 是正整数 且 n ≥ 3 ,所以只需证明 2^n > 2n + 1 ;
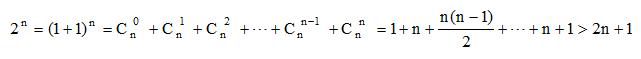
例题5图(4)
所以
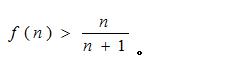
例题5图(5)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论