高考数学，典型例题分析1：客观题典型题讲解分析

典型例题分析1：

设全集U=R，集合A={y|y=x2﹣2}，B={x|y=log2（3﹣x），则（∁UA）∩B=（ ）

A．{x|﹣2≤x＜3} B．{x|x≤﹣2} C．{x|x＜﹣2} D．{x|x＜3}

解：全集U=R，集合A={y|y=x2﹣2}={y|y≥﹣2}，

∴∁UA={x|x＜﹣2}，

又B={x|y=log2（3﹣x）}={x|3﹣x＞0}={x|x＜3}，

∴（∁UA）∩B={x|x＜﹣2}．

故选：C．

考点分析：

交、并、补集的混合运算．

题干分析：

求函数的值域得集合A，求定义域得集合B，再根据补集与交集的定义写出（∁UA）∩B．

典型例题分析2：

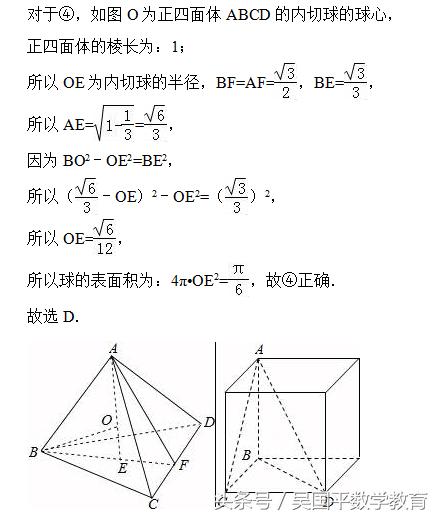
对于四面体A﹣BCD，有以下命题：①若AB=AC=AD，则AB，AC，AD与底面所成的角相等；②若AB⊥CD，AC⊥BD，则点A在底面BCD内的射影是△BCD的内心；③四面体A﹣BCD的四个面中最多有四个直角三角形；④若四面体A﹣BCD的6条棱长都为1，则它的内切球的表面积为π/6．其中正确的命题是（ ）

A．①③ B．③④ C．①②③ D．①③④

考点分析：

命题的真假判断与应用．

题干分析：

对于①，根据线面角的定义即可判断；

对于②，根据三垂线定理的逆定理可知，O是△BCD的垂心，

对于③在正方体中，找出满足题意的四面体，即可得到直角三角形的个数，

对于④作出正四面体的图形，球的球心位置，说明OE是内切球的半径，利用直角三角形，逐步求出内切球的表面积．

解题反思：

本题考查命题的真假判断与应用，综合考查了线面、面面垂直的判断与性质，考查了学生的空间想象能力，是中档题．