高中数学：导数知识知多少？

导数及其应用

第一部分知识点.

一，导数的概念及运算

2．导数的几何意义．

函数y＝f(x)在x0处的导数f′(x0)的几何意义是：曲线y＝f(x)在点(x0，f(x0))处的切线的斜率(瞬时速度就是位移函数s(t)对时间t的导数)．

二，基本初等函数的导数

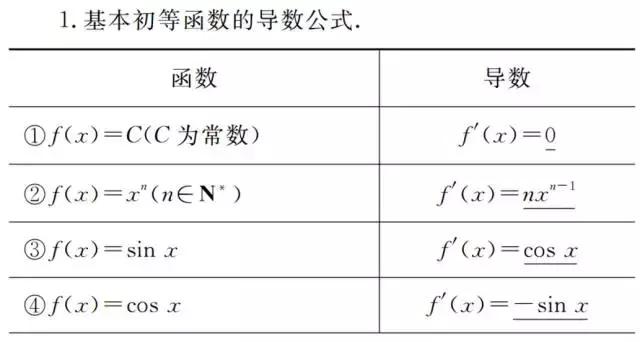
2.导数的四则运算法则．

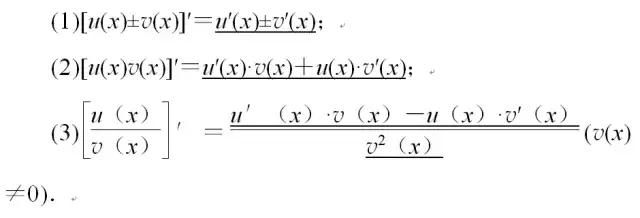
3．复合函数求导．

复合函数y＝f(g(x))的导数和y＝f(u)，u＝g(x)的导数之间的关系为yx′＝yu′·ux′．

三，导数的应用

1．函数的单调性与导数的关系．

一般地，在某个区间(a，b)内：

(1)如果f′(x)＞0⇒函数f(x)在这个区间内单调递增；

(2)如果f′(x)＜0⇒函数f(x)在这个区间内单调递减；

(3)如果f′(x)＝0⇒函数f(x)在这个区间内是常数函数．

2．函数的极值与导数的关系．

一般地，对于函数y＝f(x)：

(1)若在点x＝a处有f′(a)＝0，且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则称x＝a为f(x)的极小值点，f(a)叫函数f(x)的极小值．

(2)若在点x＝b处有f′(b)＝0，且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则称x＝b为f(x)的极大值点，f(b)叫函数f(x)的极大值．

3．求函数y＝f(x)在[a，b]上的最大值与最小值的步骤：

(1)求函数y＝f(x)在(a，b)内的极值；

(2)将函数y＝f(x)的各极值与端点处的函数值f(a)，f(b)比较，其中最大的一个是最大值，最小的一个是最小值．

四，定积分与微积分基本定理

第二部分经典例题

例3．求下列函数的导数：

(1)y＝(2x2－1)(3x＋1)；

(2)y＝x2sinx.

答案：(1)y′＝18x2＋4x－3

(2)y′＝2xsin x＋x2cos x

第三部分每日一练

一、选择题

1．函数y＝0.5x2－lnx的单调递减区间为()

A．(－1，1]

B．(0，1]

C．[1，＋∞)

D．(0，＋∞)

3．若f(x)＝－0.5x2＋bln(x＋2)在(－1，＋∞)上是减函数，则b的取值范围是( )

A．[－1，＋∞)

B．(－1，＋∞)

C．(－∞，－1]

D．(－∞，－1)

4．(2015·陕西卷)对二次函数f(x)＝ax2＋bx＋c(a为非零整数)，四位同学分别给出下列结论，其中有且只有一个结论是错误的，则错误的结论是()

A．－1是f(x)的零点

B．1是f(x)的极值点

C．3是f(x)的极值

D．点(2，8)在曲线y＝f(x)上

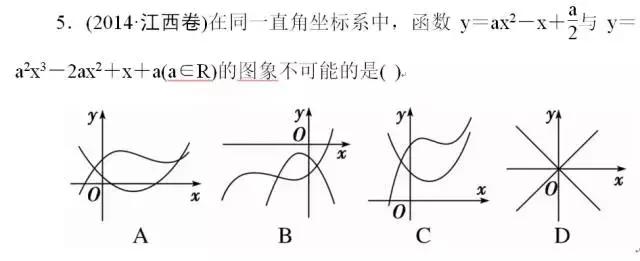
6．(2015·新课标Ⅱ卷)设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(－1)＝0，当x>0时，xf′(x)－f(x)<0，则使得f(x)>0成立的x的取值范围是()

A．(－∞，－1)∪(0，1)

B．(－1，0)∪(1，＋∞)

C．(－∞，－1)∪(－1，0)

D．(0，1)∪(1，＋∞)

二、填空题

7．(2015·陕西卷)函数y＝xex在其极值点处的切线方程为 ．

三、解答题

8．已知函数f(x)＝2x3＋ax与g(x)＝bx2＋c的图象都过点P(2，0)，且在点P处有相同的切线．

(1)求实数a，b，c的值；

(2)设函数F(x)＝f(x)＋g(x)，求F(x)的单调区间，并指出函数F(x)在该区间上的单调性．

9．(2015·新课标Ⅱ卷)设函数f(x)＝emx＋x2－mx.

(1)证明：f(x)在(－∞，0)单调递减，在(0，＋∞)单调递增；

(2)若对于任意x1，x2∈[－1，1]，都有|f(x1)－f(x2)|≤e－1，求m的取值范围．