八年级数学全等三角形问题中常见的辅助线的作法

全等三角形问题中最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等，本节来介绍下在全等三角形中常见的几种辅助线的作法：

图中有角平分线，可向两边作垂线。

线段垂直平分线，常向两端把线连。

线段计算和与差，巧用截长补短法。

三角形里有中线，延长中线至两倍。

在作辅助线的时候要注意以下两点：

①在原图形中作辅助线要用“虚线” ；②在证明过程中要描述添加方法 。

一、用角平分线的性质构造全等

例1、如图,在梯形 ABCD 中, ∠A= ∠D =90°, BE、CE 分别是∠B 和 ∠C 的角平分线 。

求证：BC= AB + CD。

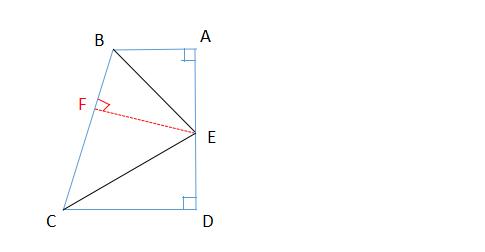
例题1图

证明：过点 E 作 EF⊥BC ，垂足为点 F

∵ BE 是 ∠B 的角平分线 ，∠EFB = ∠A = 90°

∴ EF = AE

在 △EFB 和 △EAB 中

∵ ∠EFB = ∠A = 90° ，EF = AE ，EB = EB

∴ △EFB ≌ △EAB （HL）

∴ BF = BA

同理可证 ： CF = CD

∴ BC = CF + BF = AB + CD

二、连接法

例题2、如图,在五边形 ABCDE中，点 M 是 CD 的中点， AB = AE , BC = ED ， AM⊥CD 。

求证：∠B = ∠E 。

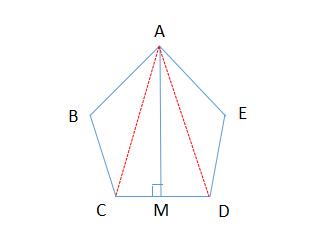
例题2图

证明：连接 AC ， AD

∵ 点 M 是 CD 的中点 ，AM⊥CD

∴ AC = AD

在 △ABC 和 △AED 中

∵ AB = AE , BC = ED，AC = AD

∴ △ABC ≌ △AED （SSS）

∴ ∠B = ∠E

三、用“截长法”或“补短法”构造全等三角形

例题3、如图，在△ABC中， AD是∠BAC的角平分线， ∠C = 2∠B 。

求证：AB = AC + CD 。

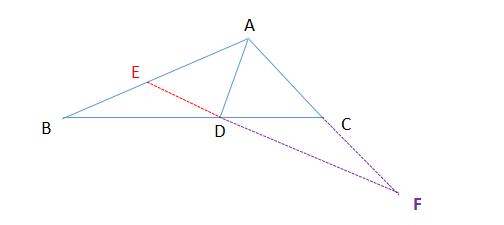
例题3图

证明：

方法一、截长法

在线段 AB 上取点 E ， 使得 AE = AC , 连接 ED

∵ AD是∠BAC的角平分线

∴ ∠EAD = ∠CAD

在 △EAD 和 △CAD 中

∵ AE = AC , ∠EAD = ∠CAD ，AD = AD

∴ △EAD ≌ △CAD

∴ ED = CD , ∠AED = ∠ACD

又 ∵ ∠AED = ∠B + ∠EDB （三角形外角和定理），∠ACD = 2∠B

∴ ∠B + ∠EDB = 2∠B （等量代换）

∴ ∠B = ∠EDB

∴ BE = ED （等角对等边）

又∵AB = AE + EB

∴ AB = AC + CD （等量代换）

方法二、补短法

延长线段 AC 至点 F ，使 CF = CD ，连接 DF

略证：

由 ∠ACB = 2∠B = ∠CDF + ∠F ， ∠CDF = ∠F

可得 ∠B = ∠F

在证 △ABD ≌ △AFD （AAS）

可得 AB = AF

而 AF = AC + CF = AC + CD

即证 AB = AC + CD

注：遇到有二条线段长之和等于第三条线段的长，常用此方法 。

四、倍长中线法构造全等三角形

例题4、如图，在 △ABC 中， AD是线段 BC 边上的中线 。

求证 ： AD < 1/2 ( AB + AC ) 。

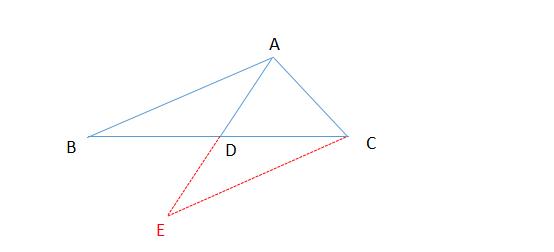
例题4图

证明：延长 AD 到点 E，使 DE= AD，连结CE

∵ AD是线段 BC 边上的中线

∴ BD = CD

在 △ADB 和 △EDC 中

∵ BD = CD ，∠BDA = ∠CDE ，AD = ED

∴ △ADB ≌ △EDC （SAS）

∴ AB = EC

在 △AEC 中

∵ EC + AC > AE （三角形中两边之和大于第三边）

又∵ AE = 2AD

∴ AB + AC > 2AD

即证 ： AD < 1/2 ( AB + AC )