绝对值不等式是不等式的补充和深化，属于选考内容，高考单独命题，常考查绝对值不等式的解法和性质的应用，难度中档。

解答含参绝对值不等式时，常常采用分类讨论法和分离参数法。分类讨论法，将绝对值不等式转化为分段函数问题来解决，而分离参数法，转化为新函数的最值或值域问题来解决。在研究恒成立问题时，常常数形结合，利用几何意义可以直观解题。

一·绝对值不等式的解法

1·零点分段法：

①令每个绝对值符号里的一次式为0，求出相应的根；

②把这些根按从小到大排列，它们把数轴分成若干个区间；

③在所分区间上，根据绝对值的定义去点绝对值符号，讨论所得不等式在这个区间上的解集；

④这些解集的并集就是原不等式的解集。

2·绝对值三角不等式：

二·高考试题剖析

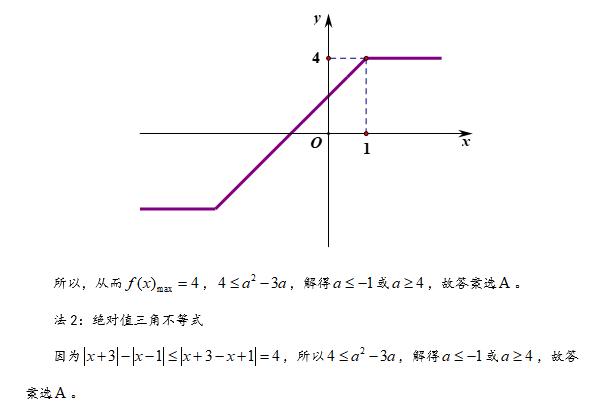
【评注】

本题就是绝对值不等式恒成立问题的典型，将不等式左端视为新函数，求出该函数的最大值，然后转化为一元二次不等式的解法。法1利用零点分段法，思路清晰，作出图象，直观明了；法2利用绝对值三角不等式，简洁迅速，二者殊途同归。在小题中，提倡用法2，节约时间。

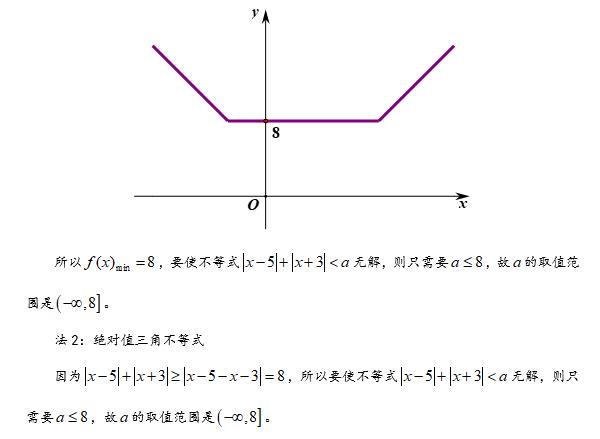
【评注】

恒成立的对立面就是无解，要使原不等式无解，只需右端比左端的最小值还小即可。于是本题转化为左端函数的最小值问题，所用方法与例题1一致。

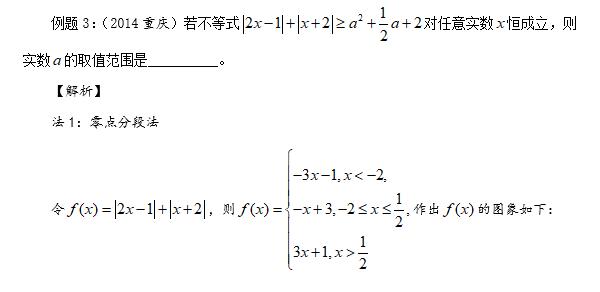
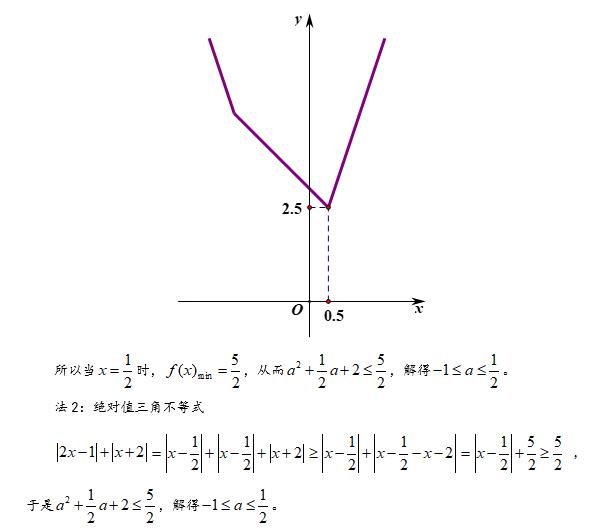
【评注】

本题中，应用零点分段法没有什么可说的，值得注意的是法2，对于变量系数不相同时，怎么拆分利用绝对值三角不等式，这是很多人都面临的困难，本题给出了答案。