「初中数学」构造K型全等

【例1】（难度系数☆☆☆☆）如图,在Rt△ABC中，∠C=90°，AC>BC，BD平分∠ABC，点E在BC上,∠EDB=45°，BE=5CE，CD=3,求AB的长。

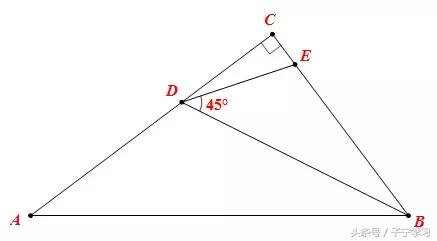
【解法一】

第一步：构造“K”字型

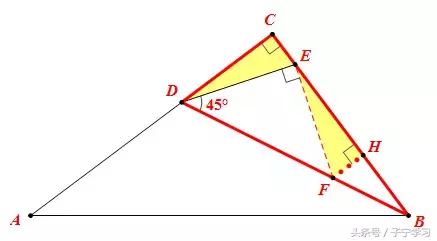
作EF⊥DE交BD于F，作FH⊥BC

∵∠BDE=45°，EF⊥DE

∴△DEF是等腰直角三角形

∴DE=DF

∵∠DEC+∠FEH=90°

∠EFH+∠FEH=90°

∴∠DEC=∠EFH

∴Rt△DEC≌Rt△EFH

∴CE=FH,EH=DC

第二步：利用“A”型相似计算

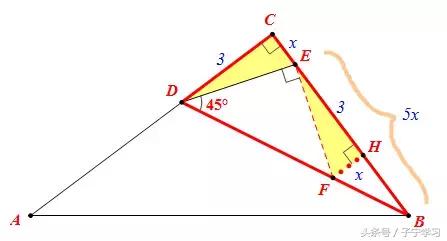
设CE=x,则BE=5x,FH=x，EH=CD=3,BH=5x-3,BC=6x

∵△BHF∽△BCD

第三步：利用“斜A型”相似求AB

当x=1时，CB=6,作DG⊥AB

∵BD平分∠ABC

∴DG=DC=3

设AG=a,AD=b

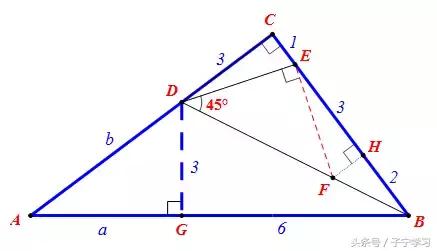
∵Rt△ADG∽Rt△ABC

当x=1.5时，不合题意，舍去。综合上述，AB=10

【解法二】

第一步：变异的"K“字型

作HB⊥DB，交DE的延长线于H，作HF⊥BC

易证Rt△BCD≌Rt△HFB

∴CD=FB，HF=BD

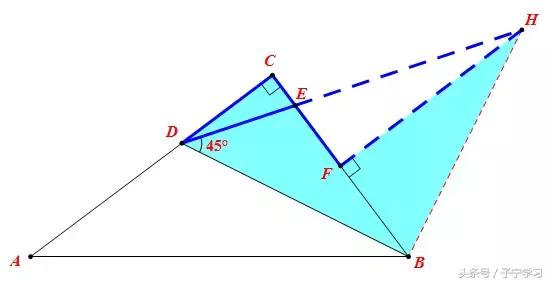
第二步：利用“X”型相似计算

设CE=x,则BE=5x,EF=5x-3,BC=HF=6x

∵Rt△CDE∽Rt△FHE

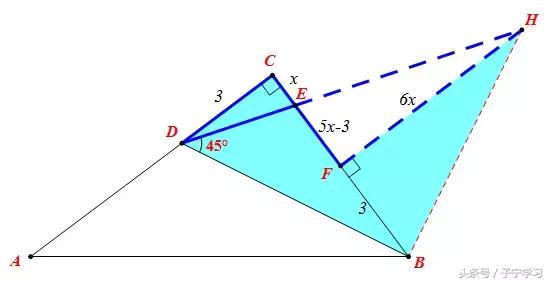
第三步：利用“斜A型”相似求AB

同方法一，略。

【总结】

此题的解法一是构造一线三直角模型之”K“字型，解法二是构造一线三直角模型之变异”K“字型，两种解法大同小异。除了构图，解题关键都离不开相似，并且大量运用了用同一个字母表示不同的线段，方程思想，勾股定理，解一元二次方程，分类讨论等，而这些恰恰是初中数学之利器，其重要性可窥一斑！建议同学们阅读之后，自己独立动手计算一遍。

【解题感悟】

四十五度有诀窍，

等腰直角少不了。

倘若仍然无法求，

再造一线三直角。