基本初等函数之一次函数与二次函数习题

1、 掌握一次函数和二次函数的性质及图象特征；

2、 运用一次函数与二次函数的性质解决有关问题。

一、知识点总结

1、一次函数

定义 ： 函数 y = kx + b ( k ≠ 0 ) 叫做一次函数，它的定义域是 R，值域是 R 。

① 一次函数的图象是直线，所以一次函数又叫线性函数；

② 一次函数 y = kx + b ( k ≠ 0 )中，k 叫直线的斜率，b 叫直线在 y 轴上的截距；

当 k > 0 时，函数是增函数 ; 当 k < 0 时，函数是减函数 。

③ 当 b = 0 时, 该函数是奇函数且为正比例函数，直线过原点；b ≠ 0 时，它既不是奇函数，也不是偶函数 。

2、 二次函数

定义： 函数 y = ax^2 + bx + c ( a ≠ 0 ) 叫做二次函数，它的定义域为是R，图象是一条抛物线 。

① 当 b = 0 时 ， 该函数为偶函数，其图象关于 y 轴对称；

②

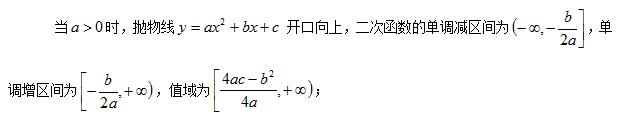
二次函数性质图（1）

③

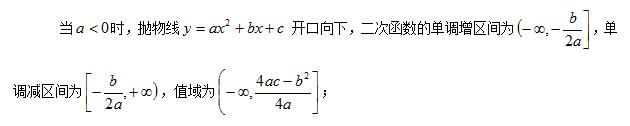
二次函数性质图（2）

④ 二次函数的三种表示形式

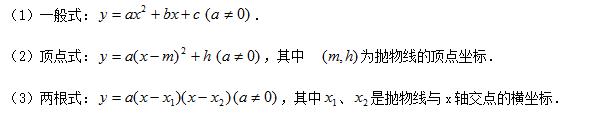
二次函数三种表示形式图（3）

⑤ 利用配方法求二次函数 y = ax^2 + bx + c ( a ≠ 0 ) 的对称轴方程为： x = -b / (2a) ；

⑥

二次函数图（4）

⑦ 用待定系数法求函数解析式时，要注意函数对解析式的要求，一次函数、正比例函数、反比例函数的比例系数、二次函数的二次项系数等；要应视具体问题，灵活地选用其形式，再根据题设条件列方程组，确定其系数。

二、典型例题

1、一次函数的性质

例1：已知函数 y＝(2m－1)x＋1－3m，求当 m 为何值时：

(1)这个函数为正比例函数？(2)这个函数为奇函数？(3)函数值 y 随 x 的增大而减小？

解：（1）由题意，得

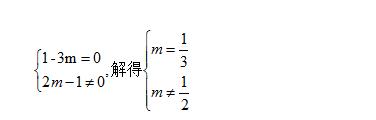
例题1图（1）

∴ m = 1/3 时 ，这个函数为正比例函数 。

（2）函数为奇函数 ，有

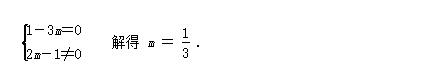
例题1图（2）

∴ m = 1/3 时 ，这个函数为奇函数 。

（3）由题意，得 2m－1<0，∴ m < 1/2

∴ m < 1/2 ， 函数值 y 随 x 的增大而减小 。

2、求一次函数的解析式

例题2、已知一次函数的图象经过点A(1,1)、B(－2,7)，求这个一次函数的解析式。

解：设 y 关于 x 的函数解析式为 y＝ax＋b (a≠0)，把 A(1,1)、B(－2,7) 的坐标分别代入 y＝ax＋b，

例题2图（1）

∴ y关于x的函数解析式为y＝－2x＋3 。

3、二次函数的值域问题

例3： 已知函数 f(x)＝x^2＋x－2，则函数 f(x) 在区间 [－1,1) 上 ( D )

A、最大值为0，最小值为－9/4 B、最大值为0，最小值为－2

C、最大值为0，无最小值 D、无最大值，最小值为－9/4

解：

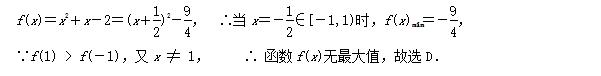
例题3图（1）

4、含参数的二次函数在闭区间上最值的讨论

例4：求 f(x)＝x^2－2ax－1 在 [0,2] 上的最大值 M(a) 和最小值 m(a) 的表达式。

解：f(x)＝(x－a)^2－a^2－1，x∈ [0,2]，

顶点是(a，－a^2－1)，二次项系数为正，图象开口向上，

对称轴 x＝a, 由 f(x) 在顶点左边 (即x ≤ a) 单调递减，在顶点右边(即x≥a)单调递增，

所以 f(x) 图象的对称轴 x＝a 与闭区间 [0,2] 的位置关系(求两种最值)分4种情况求解．如图①～④中抛物线的实线部分。

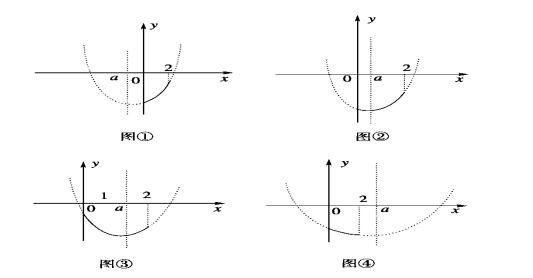
例题4图（1）

在图 ① 中，当 a < 0 时，f(x) 在 [0,2] 上单调递增，所以 M(a)＝f(2)＝－4a＋3，m(a)＝f(0)＝－1；

在图②中，当 0 ≤ a < 1，且 f(0) ≤f (2)，即0≤a<1时，f(x) 在 [a,2]上单调递增，

所以M(a)＝f(2)＝－4a＋3，m(a)＝f(a)＝－a^2－1；

在图③中，当1≤ a < 2 时，f(x)在[0，a]上单调递减，最大值M(a)＝f(0)＝－1，最小值m(a)＝f(a)＝－a^2－1；

在图④中，当a ≥ 2 时，f(x) 在 [0,2] 上单调递减，所以M(a)＝f(0)＝－1，m(a)＝f(2)＝－4a＋3。