基本初等函数专题训练

一、知识体系图

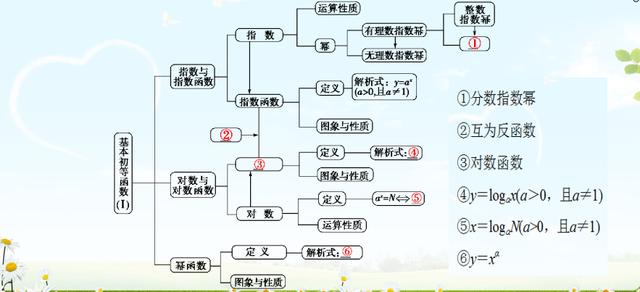
基本初等函数知识体系图

二、专题训练

1、指数、对数的运算

解决这类问题首先要熟练掌握指数式、对数式的运算法则，熟练掌握各种变形，进行相互之间的转化，选择适合题目的形式进行运算。

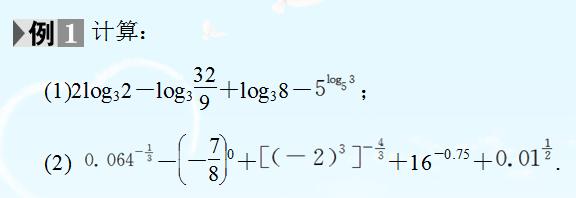
例题1图（1）

解题思路：

（1）利用对数的运算法则、对数恒等式即可得出；

（2）利用指数幂的运算法则即可得出。

解答过程：

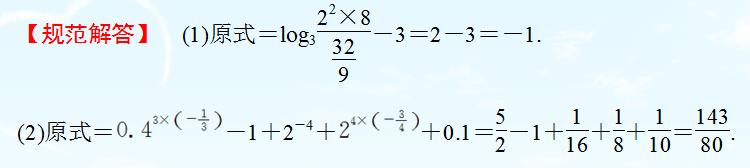
例题1图（2）

2、指数、对数型函数的定义域、值域

求定义域主要通过构建不等式（组）来求解，有时解不等式（组）时要借助于指数、对数函数的单调性。

涉及值域问题主要有两个 类型：

一是形如 y = a^[f(x)] 和 y = logaf(x) 的函数，一般要先求出 f(x) 的值域，然后利用指数、对数函数的单调性求解；

二是形如 y = f(a^x) 和 y = f(logax) 的函数，则要根据 a^x 和 logax 的范围，利用函数 y = f(x) 的性质求解 。

例题2图（1）

解题思路：

（1）令 t = x^2 -2x +2 , 则 y = (1/2)^t ，根据 x 的范围求出 t 的范围，可得函数 y = (1/2)^t 的范围；

（2）结合二次函数的性质即可求解 。

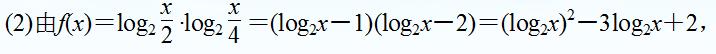
例题2图（2）

解答过程：

例题2图（3）

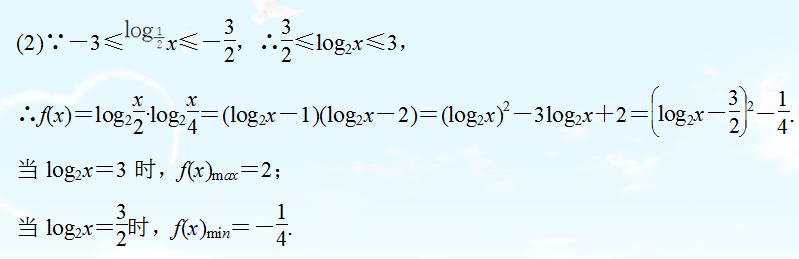
例题2图（4）

3、幂、指数、对数函数的图象和性质

解决此类问题要熟练掌握幂、指数、对数函数的图象和性质，方程与不等式的求解可利用函数的单调性进行转化，也可利用图像解决，对含参数的问题进行分类讨论，同时还要注意变量本身的取值范围，以免出现增根。

例题3图（1）

解题思路：

由指数函数和对数函数的图像和性质，将已知不等式转化为不等式恒成立问题加以解决即可。

解答过程：

例题3图（2）

4、比较大小问题

数的大小比较常用方法：

①单调性法、图像法、作差法、作商法、中间搭桥法；

②当需要比较大小的两个实数均是指数幂或对数式时，可将其看成某个指数函数、对数函数或幂函数的函数值，然后利用该函数的单调性作比较；

③比较多个数的大小时，先利用 “0” 和 “1” 作为分界点，即把它们分为 “小于 0 ” 、“大于等于 0、小于等于 1 ” 、“大于 1” 三部分，然后再在各部分内利用函数的性质比较大小 。

例题4图（1）

解题思路：

利用指数函数、对数函数和幂函数的性质进行比较大小。

解答过程：

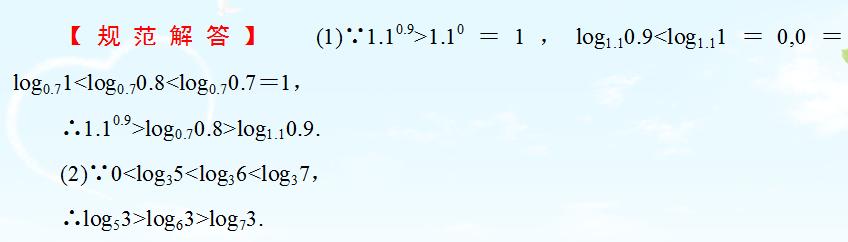
例题4图（2）

5、分类讨论思想

在初等函数中，分类讨论的思想得到了重要的体现，可根据函数的图像和性质，依据函数的单调性进行分类讨论，使求解得以实现。

例题5图（1）

解题思路：

（1）结合 f(3) < f(5) 与函数 f (x ) 的奇偶性，分类讨论确定 m 的值及 f (x) 的解析式；

（2）由 g (x ) 为增函数，结合 a 讨论，求出 a 的取值范围 。

解答过程：

例题5图（2）

例题5图（3）

例题5图（4）