柯西不等式在解决高中数学问题中具有较好的效果,而柯西不等式的向量形式在解答过程中具有简洁、明了、给人耳目一新的感觉。
本文给出向量的两条性质,并举例说明这两条性质在解题中的应用。
首先,给出以下性质1
性质1 m·n≤|m|·|n| ,当m与n同向时取“ =”.



性质2
若|m|=|n|,且m·n=|m|·|n|,则 m=n.

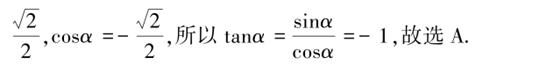


以上几例说明,要善于观察题目特征,构造恰当的向量并利用向量性质来解题,该解法思考方式新颖并且富有创造性,使解题难点转移,使解题过程优化.

高考热点:向量的两个性质在解题中的应用
柯西不等式在解决高中数学问题中具有较好的效果,而柯西不等式的向量形式在解答过程中具有简洁、明了、给人耳目一新的感觉。
本文给出向量的两条性质,并举例说明这两条性质在解题中的应用。
首先,给出以下性质1
性质1 m·n≤|m|·|n| ,当m与n同向时取“ =”.



性质2
若|m|=|n|,且m·n=|m|·|n|,则 m=n.

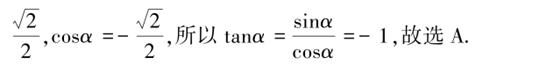


以上几例说明,要善于观察题目特征,构造恰当的向量并利用向量性质来解题,该解法思考方式新颖并且富有创造性,使解题难点转移,使解题过程优化.

2019版高考物理一轮复习高频考点强化二受力与平衡问题练习
高考重点词汇provide、providing和provided用法辨析
高考重点词汇provide、providing和provided用法辨析
高考导数压轴题——端点效应
 加载中,请稍侯......
加载中,请稍侯......
精彩评论