三角形什么时候可以用余弦定理？

我们知道在正弦定理中：

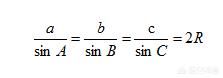
正弦定理图（1）

可以解决两类三角形的问题：

① 已知两角和任意一边，求其它边与角；

② 已知两边和一边的对角，求其它边与角 。

那么还能用正弦定理解决如下的问题吗？

①已知： a = 1 , b = 5 , ∠C = 60° ，求 c ?

②已知 ：a = 2 , b = 2 , c = 2√3 , 求 ∠C ？

答案是不能解决，为了解决遇到的此类问题，我们还要继续研究有关的定理——“余弦定理”。

余弦定理：

三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。

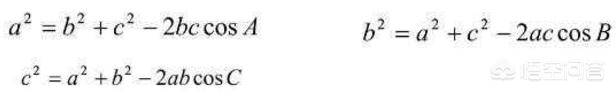
余弦定理图（2）

从上面的式子中我们发现共有“四个量”，从方程的角度看如果知道其中任意三个量，便可以求第四个量。

那么能否由三边求出一角呢？

从上面的余弦定理中可以得到以下的推论：

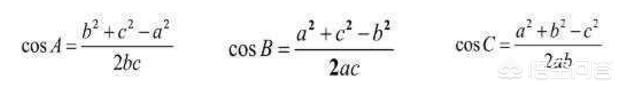
余弦定理推论图（3）

这样我们就知道了什么时候应用余弦定理，同样“余弦定理”解决两类解三角形的问题：

①已知两边及其夹角求第三边；

②已知三边求三角。

知识应用：

例题1、有三个小村庄 A、B、C 已知村庄 AB 之间相距 10 千米，村庄 BC 之间相距 12 千米，且测得 ∠ABC = 60° ， 求村庄 A 与村庄 C 之间的距离 。

分析：从实际问题中抽象出数学问题：已知两边及其夹角求第三边的问题，直接用余弦定理求解。

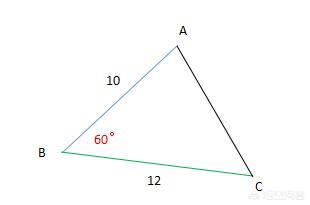
例题图（4）

解答：略。

例题2、如果在上面的例题中知道了三边的长度，我们就可以通过“余弦定理”求出任意两边的夹角。

综上所述：

在任意三角形中：

①已知两边及其夹角求第三边；

②已知三边求三角。

只要满足上述条件，就可以用“余弦定理”求解。